AHS (Alexander Horned Sphere)

J. W. Alexander 构造了一个单连通曲面, 其(外面)所围区域非单连通. 文章很短, 见 [1].

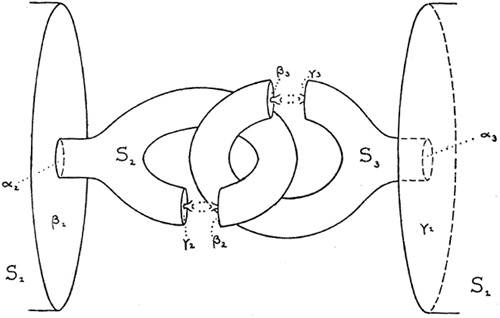
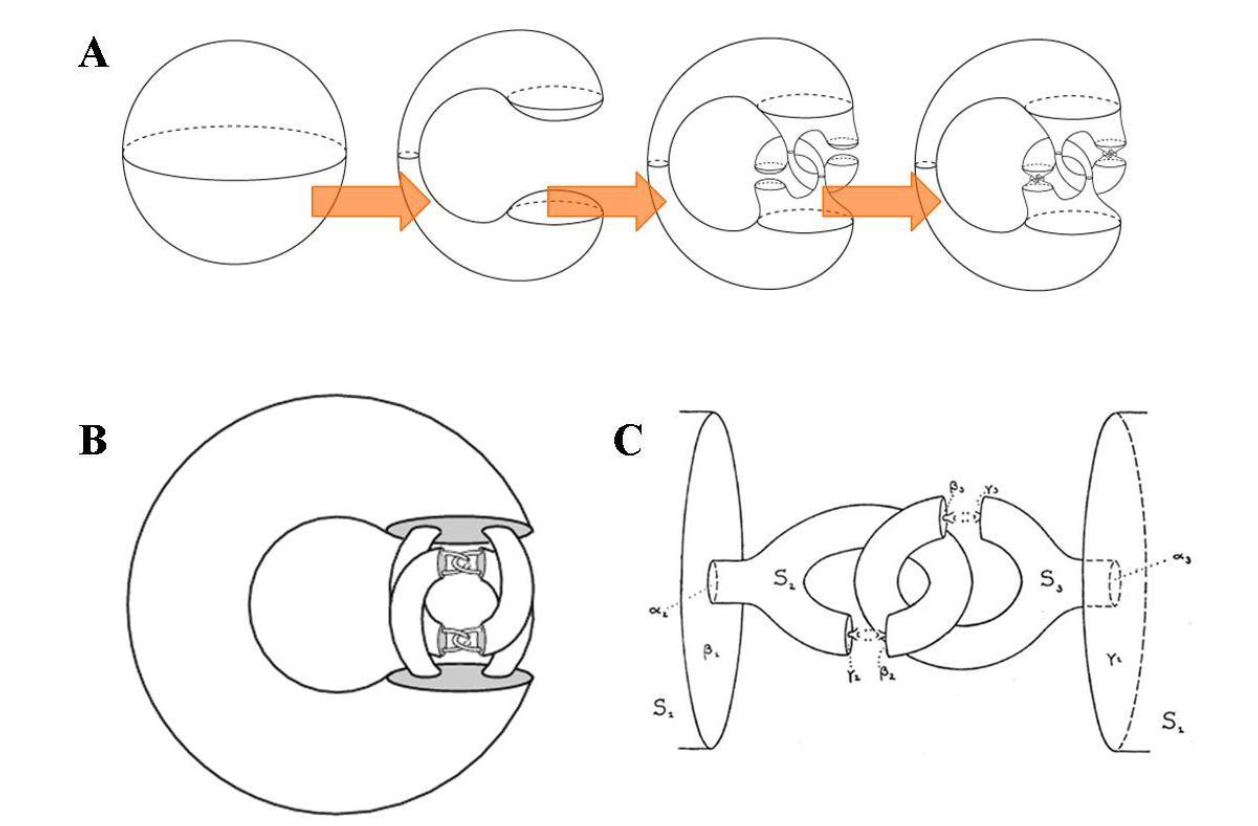
具体的构造如下:

References:

[1]  J. W. Alexander, Proceedings of the National Academy of Sciences of the United States of America, Jan. 15, 1924, Vol. 10, No. 1 (Jan. 15, 1924), pp. 8--10.

三维欧氏空间中一个多面体假设有 $7n$ 个面, 证明: 存在 $n+1$ 个面, 这 $n+1$ 个面有相同的边数(即都是 $m$-边形).

[Hint]  利用欧拉公式.

设 $V,E,F$ 分别表示一个多面体的顶点数、边数和面数, 则欧拉公式为

\[V-E+F=2.\] 

题目来源:

Bilibili,  Up:  RealFiddie

构建开球 $\mathrm{int}(D^n)$ 到 $\mathbb{R}^n$ 的同胚映射.

这里 $D^n=\{x\in\mathbb{R}^n\mid |x|\leqslant 1\}$, $\mathrm{int}(D^n)$ 是 $D^n$ 的内部. 有时也记

\[
B^n=\{x\in\mathbb{R}^n\mid |x| < 1\},
\]

即 $B^n=\mathrm{int}(D^n)$, 而 $\bar{B}^n=D^n$.

[Hint] 利用 $y=\tan x$, $x\in(-\frac{\pi}{2},\frac{\pi}{2})$, 可以构建 $(-1,1)$ 到 $\mathbb{R}$ 的同胚映射:

\[
\begin{array}{rcl}
\varphi:\ (-1,1)&\rightarrow&\mathbb{R}\\
x&\mapsto&\tan(\frac{\pi}{2}x)
\end{array}
\]

CW 复形(CW complex)

设 $X$ 为拓扑空间. 集合 $A\subset X$ 如果称为 $X$ 的子空间, 则要求 $A$ 具有诱导拓扑(或相对拓扑, 即 $U$ 是 $A$ 中的开集, 如果存在 $V\in\tau_{X}$, 使得 $U=V\cap A$.)

$\mathbb{E}^n=(\mathbb{R}^n,d)$ 是 $n$ 维欧氏空间, 当然是度量空间, 从而也是拓扑空间. $\mathbb{E}^n$ 中的一个 $n$-维(闭)球是指

\[
D^n=\{x\in\mathbb{E}^n\mid |x|\leqslant 1\}
\]

References:

Soren Hansen,  CW complexes.

The Eckmann–Hilton argument

https://ncatlab.org/nlab/show/Eckmann-Hilton+argument

[吴文俊] $S^{4k}$ 不是近复流形.

证明: 利用示性类.

利用同伦论的 Steenrod 平方运算, Borel-Serre 证明了:  $S^{2n}$, $n>0, n\neq 3$ 不是近复流形.

References:

S. S. Chern 93岁时的演讲

https://www.zhihu.com/question/52146571

利用拓扑 K 理论证明: 若 $n > 3$, 则 $S^{2n}$ 上不存在近复结构.

证明: $\mathbb{R}^n$ 与 $\mathbb{R}^m$ 同胚仅当 $n=m$.

类似的, 当 $n\neq m$ 时, $S^n$ 与 $S^m$ 也不同胚.