1. 关于图论的算法
Posted by haifeng on 2022-10-15 15:11:09 last update 2022-10-15 15:14:02 | Answers (0) | 收藏
Posted by haifeng on 2022-10-15 15:11:09 last update 2022-10-15 15:14:02 | Answers (0) | 收藏
Posted by haifeng on 2022-10-15 13:36:36 last update 2022-10-15 15:09:50 | Answers (0) | 收藏
以下内容是阅读 [1] 后的笔记.
$G=(V,E)$ , $V$ 指顶点集, $E$ 是 $V$ 的二元无序(或有序)配对集的子集, 即
\[
E\subset\{[v_i, v_j]\ :\ v_i, v_j\in V\}
\]
无序配对指 $[v_i, v_j]=[v_j, v_i]$. 此时图 $G$ 称为无向图.
如果 $[v_i,v_j]$ 中 $v_i$ 是起点或源点, $v_j$ 是终点, 则称 $[v_i,v_j]$ 是有向边, 图 $G$ 是有向图.
| 记号 | 含义 | 英文 |
|---|---|---|
| $V(G)$ | 图 $G$ 的顶点集 | |
| $E(G)$ | 图 $G$ 的边的集合 | |
| $|V|$ | 集合 $V$ 中元素个数, 即顶点个数 | |
| $|E|$ | 集合 $E$ 中元素个数, 即边的条数 | |
| $|G|$ | 定义为 $|V(G)|$, 即图 $G$ 中顶点个数, 称为图 $G$ 的阶. | order of $G$ |
| $e(G)$ | 图 $G$ 中边的条数, 即 $|E(G)|$. | size of $G$ |
| $x\in G$ | 如果 $x$ 是 $G$ 的一个顶点, 即 $x\in V(G)$, 通常简写为 $x\in G$. | |
| $xy$ | 边 $xy$ | |
| $G^n$ | 阶为 $n$ 的图 $G$. | |
| $G'\subset G$ | 图 $G'=(V',E')$ 是图 $G=(V,E)$ 的子图, 即要求 $V'\subset V$ 且 $E'\subset E$. | subgraph |
| $G\cong H$ | 两个图同构, 可以简写为 $G=H$. | $G$ is isomorphic to $H$ |
| $\Gamma(x)$ | 与顶点 $x$ 关联的点之集. | set of adjacent points of vertex $x$. |
| $d(x)$ | 顶点 $x$ 的度, 即定义为 $d(x)=|\Gamma(x)|$. | degree of vertex $x$ |
| $d^{+}(x)$ | $x$ 的出度, 即 $d^{+}(x)=|\{y\in\Gamma(x)\mid \overrightarrow{xy}\in E\}|$ | |
| $d^{-}(x)$ | $x$ 的入度, 即 $d^{-}(x)=|\{y\in\Gamma(x)\mid \overrightarrow{yx}\in E\}|$ | |
| $\delta(G)$ | $G$ 的最小度. | minimal degree |
| $\Delta(G)$ | $G$ 的最大度. | maximum degree |
通常我们考虑有限图, 即 $|V(G)|$ 和 $|E(G)|$ 均有限的图.
基本概念
Def. (同构) 图 $G=(V,E)$ 与 $G'=(V',E')$ 同构是指存在一个双射 $\phi: V\rightarrow V'$, 使得 $xy\in E$ 当且仅当 $\phi(x)\phi(y)\in E$.
显然, 同构的图拥有相同的阶和大小. 通常我们不区分两个同构的图, 除非图中有特定的标记的情况下.
Def. 度为 0 的点称为孤立点(isolated vertex).
Def. ($k$-正规图) 若 $\delta(G)=\Delta(G)=k$, 也即 $G$ 中每个顶点的度为 $k$, 则称图 $G$ 是 $k$-正规图($k$-regular graph), 或度为 $k$ 的正规图.
一个 $3$-正规图被称为立方图(cubic graph).
基本性质
Claim 1. $n$ 阶图 $G$ 的大小(size) 在 $0$ 和 $C_n^2=\frac{n(n-1)}{2}$ 之间.
Def. 大小为 $\binom{n}{2}$ 的图称为 $n$ 阶完全图(complete $n$-graph), 记作 $K^n$.
$n$ 阶空图指仅有 $n$ 个顶点, 边数为 0 的图, 记为 $E^n$.
Prop. 设 $G$ 是 $k$-正规图, 若 $k$ 是奇数, 则 $|G|$ 必是偶数.
Pf. 记 $m=|G|$, 则 $|E(G)|=\frac{m\cdot k}{2}$, 而 $k$ 是奇数, 故 $m$ 是偶数.
References:
[1] Béla Bollobas, Graph Theory -- An Introductory Course. GTM 63.
Posted by haifeng on 2019-04-25 21:10:32 last update 2019-04-26 12:47:26 | Answers (0) | 收藏
Floyd 算法是图论中计算两两顶点之间最短路径的算法. 算法复杂度为 $O(N^3)$.
设 $G=(V,E)$ 是一个带权图(有向或者无向). $n=|V|$, $W$ 是它的权矩阵. 顶点集合 $V=\{v_1,v_2,\ldots,v_n\}$, 有时不妨记为 $V=\{1,2,\ldots,n\}$.
通过下面的算法计算距离矩阵 $D=(d_{ij})_{n\times n}$ 和路径矩阵 $R=(r_{ij})_{n\times n}$.
其中 $d_{ij}=\text{dist}(v_i,v_j)$. 而 $r_{ij}$ 表示顶点 $v_i$ 到 $v_j$ 的最短路径中经过的某个顶点.
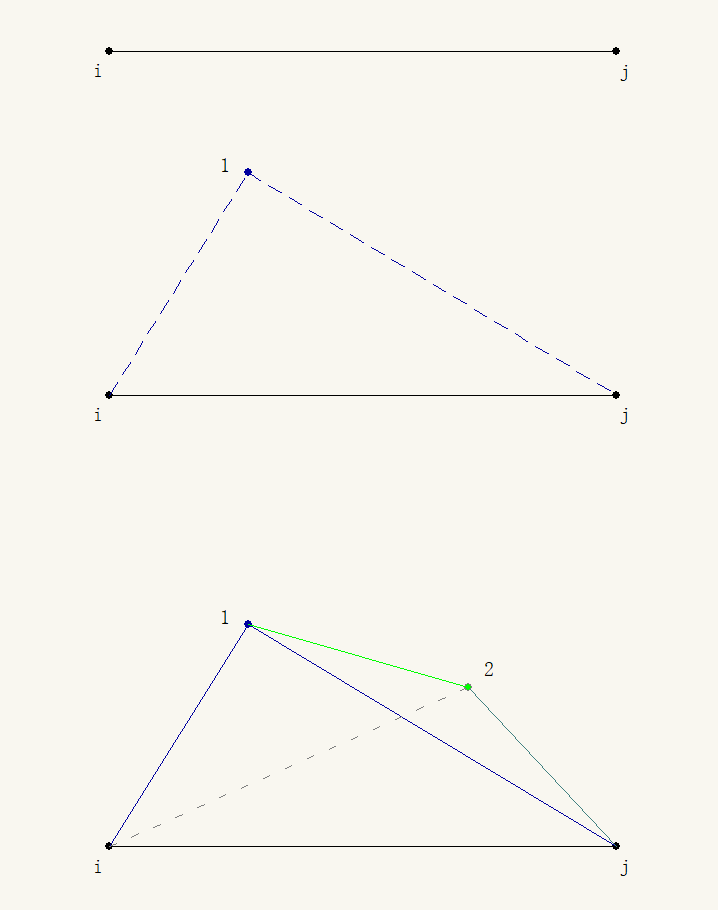
(1)第一幅图. 线段 $i--j$
$d_{ij}^{(0)}=d(i,j)$ 指顶点 $v_i$ 和 $v_j$ 之间的权, 初始矩阵 $D^{(0)}=(d_{ij}^{(0)})=W$.
(2) 第二幅图. 三角形 $ij1$. 在 $v_i$ 和 $v_j$ 之间插入了顶点 $v_1$.
\[
d_{ij}^{(1)}=\min\{d_{ij}^{(0)},d_{i1}^{(0)}+d_{1j}^{(0)}\}
\]
也就是说, 从 $v_i$ 到 $v_j$ 的最短路径必从三角形 $ij1$ 的边界(boundary)上经过.
(3) 第三幅图. 四面体 $ij12$(也就是三维单形)
从 $v_i$ 到 $v_j$ 的最短路径, 先考虑从 $\triangle i21$ 的边界(boundary)经过, 然后从 $\triangle 2j1$ 的边界(boundary)经过. 将它们的和与 $d_{ij}^{(1)}$ 作比较. 取长度较小的路径.
实际上, 从 $v_i$ 到 $v_j$ 的最短路径, 必从四面体 $ij12$ 的三个面 $i21$, $2j1$, $ij1$ 所组成的复形的骨架上经过. 当然这样的话, 已经将三角形 $ij2$ 的边界考虑了. 因此, 从 $v_i$ 到 $v_j$ 的最短路径必从四面体 $ij12$ 的边界上经过.
其余的, 可从高维上类似理解.
以下是 MATLAB 代码
% page 93.
% filename: floyd.m
function [D,R] = floyd(A)
n=size(A,1); % n 等于矩阵 A 的行数.
D=A
for i=1:n
for j=1:n
R(i,j)=j;
end
end
R
for k=1:n
for i=1:n
for j=1:n
if D(i,k)+D(k,j) < D(i,j)
D(i,j)=D(i,k)+D(k,j);
R(i,j)=R(i,k);
end
end
end
k
D
R
'-----------------------'
end
注意:
Posted by haifeng on 2019-04-25 18:05:34 last update 2019-04-25 18:06:13 | Answers (0) | 收藏
设 $G=(X,Y,E)$ 是二元图, $M$ 是图 $G$ 的一个匹配, $K$ 是图 $G$ 的一个覆盖. 则 $M,K$ 分别是图 $G$ 的最大匹配、最小覆盖的充要条件是: $|M|=|K|$.
References:
赵静、但琦 主编《数学建模与数学实验》(第4版) P.102
Posted by haifeng on 2019-04-25 18:03:40 last update 2019-05-09 17:26:26 | Answers (2) | 收藏
对二元图 $G=(X,Y,E)$, 有
(1) $G$ 存在饱和 $X$ 中每个顶点的匹配的充要条件是
\[
|N(S)|\geqslant|S|,\quad\forall\ S\subset X.
\]
其中 $N(S)=\{v\in Y\mid \exists u\in S, u\ \text{与}\ v\ \text{相邻}\}$.
(2) $G$ 存在完美匹配的充要条件是
\[
|N(S)|\geqslant|S|,\quad\forall\ S\subset X.
\]
(3) 若存在正整数 $t$, 满足 $\forall v\in X, d(v)\geqslant t$, $\forall u\in Y, d(u)\geqslant t$, 则存在饱和 $X$ 中每个顶点的匹配.
Remark:
基本概念:
点的邻域(neighborhood), 设 $x\in G$, 与 $x$ 相邻的所有顶点的集合记为 $\Gamma(x)$.
偶尔地, 称 $\Gamma(x)$ 为顶点 $x$ 的开邻域(open neighbourhood), 而将 $\Gamma(x)\cup\{x\}$ 称为 $x$ 的闭邻域(closed neighbourhood).
References:
赵静、但琦 主编《数学建模与数学实验》(第4版) P.102
GTM 184, Béla Bollobas, Modern Graph Theory
Posted by haifeng on 2018-05-10 18:40:13 last update 2018-05-10 18:40:59 | Answers (0) | 收藏
旅行商问题(TSP) 也称旅行售货员问题
设 $c_1,c_2,\ldots,c_n$ 是 $n$ 个不同的城市. 有个售货员居住在某个城市 $c_{i_0}$, 他从 $c_1$ 出发到其他城市 $c_2,\ldots,c_n$ 去推销商品(货物), 最后要回到城市 $c_{i_0}$.
假定任意两个城市间的距离是已知的, $d_{ij}:=d(c_i,c_j)$.
问他应沿着怎样的路线走, 才能使得所走的路线最短?
References:
赵静、但琦主编《数学建模与数学实验》(第四版)P.106--107
宋增民 主编 《图论及其应用》1.1.3
Posted by haifeng on 2018-05-10 18:27:58 last update 2018-05-10 18:41:27 | Answers (0) | 收藏
问题描述:
邮递员发送邮件时, 要从邮局出发, 经过他投递范围内的每条街道至少一次, 最后返回邮局. 邮递员希望能选择一条行程最短的路线.
模型
这里用点表示交叉路口, 点与点之间的连线(边)表示街道. 每条边赋予一个数(权)表示街道的长度.
这个问题是遍历所有边且使得权最小的问题.
Remark:
由于此问题是由中国的管梅谷教授首先研究的, 国际上通称为中国邮递员问题.
References:
赵静、但琦主编《数学建模与数学实验》(第四版)P.104
宋增民 主编 《图论及其应用》1.1.2
Posted by haifeng on 2018-04-11 10:36:56 last update 2018-04-17 17:04:19 | Answers (0) | 收藏
所谓的路径(path)是指一个图 $P$, 满足
\[
V(P)=\{x_0,x_1,\ldots,x_{\ell}\},\quad E(P)=\{x_0x_1, x_1x_2,\ldots,x_{\ell-1}x_{\ell}\}.
\]
这里 $x_i\neq x_j$, $\forall\ i\neq j$.
这条路径 $P$ 通常记为 $x_0x_1x_2\ldots x_{\ell}$. 顶点 $x_0$ 和 $x_{\ell}$ 是路径 $P$ 的两个端点. 而 $\ell=e(P)$ 是路径 $P$ 的长度.
我们称 $P$ 是从 $x_0$ 到 $x_{\ell}$ 的一条路径(path), 或简记为 $x_0-x_{\ell}$ path. 当然 $P$ 也是一条从 $x_{\ell}$ 到 $x_0$ 的路径, 或简记为 $x_{\ell}-x_0$ path.
有时, 我们将强调 $P$ 是从 $x_0$ 到 $x_{\ell}$ 的, 并且称 $x_0$ 为起点(或始点)(initial vertex), $x_{\ell}$ 为终点(terminal vertex).
以 $x$ 为起点的道路称为 $x$-path.
大多数路径可以视为某给定图 $G$ 的一个子图. 图 $G$ 的一条通路(walk)是指一条由顶点与边组成的交错序列:
\[
x_0,\alpha_1,x_1,\alpha_2,x_2,\ldots,\alpha_{\ell},x_{\ell}.
\]
其中 $\alpha_i=x_{i-1}x_i$, $i=1,2,\ldots,\ell$. 这里顶点和边都可以重复.
$\ell$ 称为这条通路(walk)的长度.
如果通路(walk)中限定边不能重复, 顶点可以重复, 则称这条通路为道路(trail).
因此, 所谓的路径, 实际上就是顶点和边均不重复的通路.
若道路(trail)的两端点重合(也即是一条闭合道路 a closed trail),则称其为一个回路(circuit).
设 $W=x_0x_1\ldots x_{\ell}$ 是一条通路(walk), 满足 $\ell\geqslant 3$, $x_0=x_{\ell}$. 并且诸 $x_i(0 < i < \ell)$ 互不相同, 也不同于 $x_0$, 则称 $W$ 是一个 圈(cycle).
为简单起见, 这个 cycle 记为 $x_1x_2\ldots x_{\ell}$. 注意到这里的记号不同于之前的, 这里 $x_1x_{\ell}$ 也是该 cycle 的一条边. 进一步的, $x_1x_2\ldots x_{\ell}$, $x_{\ell}x_{\ell-1}\ldots x_1$, $x_2x_3\ldots x_{\ell}x_1$, $x_ix_{i-1}\ldots x_1x_{\ell}x_{\ell-1}\ldots x_{i+1}$ 都指的是同一个 cycle.
记号:
| 符号 | 涵义 |
|---|---|
| $P^{\ell}$ | 长度为 $\ell$ 的一条路径(path) |
| $C^{\ell}$ | 长度为 $\ell$ 的一个圈 (cycle) |
我们称 $C^3$ 是一个三角形(triangle), $C^4$ 是一个四边形(quadrilateral), $C^5$ 是一个五边形(pentagon), 等等.
一个 cycle 被称为是 even (或 odd) 的, 如果它的长度是 even (或 odd) 的.
给定顶点 $x,y$, 它们之间的距离 $d(x,y)$ 指连接这两点的所有路径中长度最短的那条路径的长度.
\[
d(x,y)=\min\{\text{length of } x-y\ \text{path}\}
\]
若 $x,y$ 之间不存在 $x-y$ path, 则令 $d(x,y)=\infty$.
一个图称为是连通的(connected), 如果对于任意两个不同点组成的点对 $\{x,y\}$, 都存在一条从 $x$ 到 $y$ 的路径(path).
设无向图 $G(V,E)$ 是连通的, 设边集 $E_1\subset E$. 在图 $G$ 中删除 $E_1$ 中所有的边后得到的子图是不连通的, 而删除了 $E_1$ 的任一真子集后得到的子图是连通图, 则称 $E_1$ 是 $G$ 的一个割边集.
若割边集仅由一条边组成, 则称这条边为割边, 或桥(bridge).
References:
Béla Bollobas, Graph Theory, An introductory course. GTM 63.
Posted by haifeng on 2018-04-10 23:04:20 last update 2018-04-10 23:04:20 | Answers (1) | 收藏
定理. 设 $M$ 是图 $G$ 的匹配, $K$ 是覆盖, 则:
(1) $|M|\leqslant |K|$;
(2) 若 $|M|=|K|$, 则 $M$ 是最大匹配, $K$ 是最小覆盖.
Posted by haifeng on 2014-04-14 09:22:08 last update 2014-04-14 09:22:47 | Answers (0) | 收藏
将一个图 $G$ 的各顶点着色, 使相邻顶点不同颜色的最少颜色数, 称为该图的 chromatic number.
References: