(1) 设 $M$ 是 $G$ 中饱和 $X$ 中每个顶点的匹配.
$G$ 是二元图, 因此 $X$ 中的顶点互不相邻. 又 $M$ 是匹配, 所以 $M$ 中的边互不相邻. 于是任取 $S\subset X$, 对任意 $u\in S$, 通过 $M$, 存在 $v\in Y$ 与之相邻. 而这些 $v\in N(S)$. 因此 $|N(S)|\geqslant|S|$.
反之, 假设 $\forall\ S\subset X$, 有 $|N(S)|\geqslant|S|$. 可用归纳法构造出饱和 $S$ 的一个匹配.
具体的, 设 $X=\{u_1,u_2,\ldots,u_n\}$.
任取点 $u_1\in X$, 根据假设, $u_1$ 的邻居(neighbor)数量至少是 1. 因此不妨设为 $v_1\in Y$. 然后任取 $u_2\in X-\{u_1\}$, 对于 $S=\{u_1,u_2\}$, 根据假设, $u_1,u_2$ 的邻居数量至少为 2. 如果 $u_2$ 仅有的邻居也是 $v_1$, 那么 $u_1$ 的邻居除了 $v_1$ 之外还有另外一点 $v_2$. 若 $u_2$ 不与 $v_1$ 相邻, 则必与另外一点(不妨仍记为) $v_2$ 相邻.
对于前一种情况, 取 $e_1=(u_1,v_2)$, $e_2=(u_2,v_1)$; 第二种情况, 取 $e_1=(u_1,v_1)$, $e_2=(u_2,v_2)$. 于是由 $e_1,e_2$ 所构成的边集 $M$ 即为饱和 $S$ 的一个匹配.
我们假设当 $|X|=k$ 时, 结论成立. 也即, 若对 $\forall\ S\subset X$ 都有 $|N(S)|\geqslant |S|$, 则可以找到一个饱和 $X$ 的匹配.
现在考虑 $|X|=k+1$ 的情形. 对于 $X$ 的其元素个数为 $k$ 的任意子集 $S=\{u_1,u_2,\ldots,u_k\}$, 序号经过适当重排, 总可以找到一个饱和 $S$ 中所有顶点的匹配 $M=\{e_1,e_2,\ldots,e_k\}$, 这里 $e_i=(u_i,v_i)$. $v_i\in Y$, $i=1,2,\ldots,k$.
记 $u_{k+1}$ 是 $X-S$ 中的唯一的顶点. 若 $u_{k+1}$ 与 $\{v_1,v_2,\ldots,v_k\}$ 之外的 $Y$ 中的顶点相邻, 不妨记为 $v_{k+1}$, 那么令 $e_{k+1}=(u_{k+1},v_{k+1})$ 即可, 并加入到 $M$ 中, 即得到饱和 $X$ 的一个匹配.
如果 $u_{k+1}$ 的邻居都是 $\{v_1,v_2,\ldots,v_k\}$ 中的点. 则 $\{u_1,u_2,\ldots,u_k\}$ 中必存在某个顶点与 $\{v_1,v_2,\ldots,v_k\}$ 之外的顶点相邻, 否则就违反假设. 不妨设某个 $u_{j_0}$ 与 $\{v_1,v_2,\ldots,v_k\}$ 之外的顶点相邻, 不妨仍记为 $v_{k+1}$. 则令 $e_{j_0}=(u_{j_0},v_{k+1})$. 如果 $v_{j_0}$ 正好是 $u_{k+1}$ 的邻居, 则令 $e_{k+1}=(u_{k+1},v_{j_0})$. 则 $M$ 已经取好.
如果 $v_{j_0}$ 不是 $u_{k+1}$ 的邻居. 比如 $u_{k+1}$ 与 $v_{j_1}$ 相邻.
例如下图, $k=3$ 的情形, 很好证明.
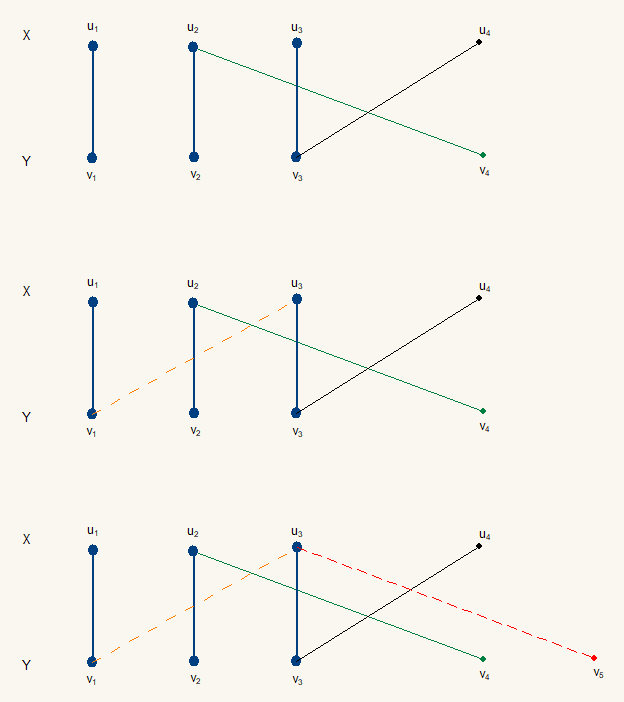
一般情形:
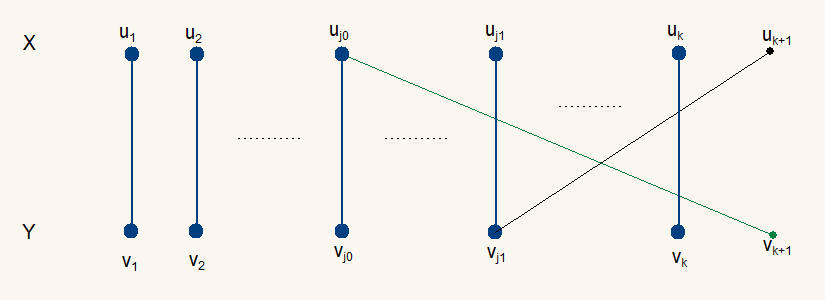
因此, 对于 $S=\{u_1,u_2,\ldots,u_n\}=X$, 存在 $T=\{v_1,v_2,\ldots,v_n\}\subset Y$, 这里序号经过重新排序, 使得其中的 $u_i$ 与 $v_i$ 相邻. 令 $M=\{e_i\mid i=1,2,\ldots,n\}$, 则 $M$ 是图 $G$ 的饱和 $X$ 中每个顶点的一个匹配.

