1. 球面几何之应用,求日出日落时间的问题
Posted by haifeng on 2019-02-14 10:40:17 last update 2019-02-14 10:50:16 | Answers (0) | 收藏
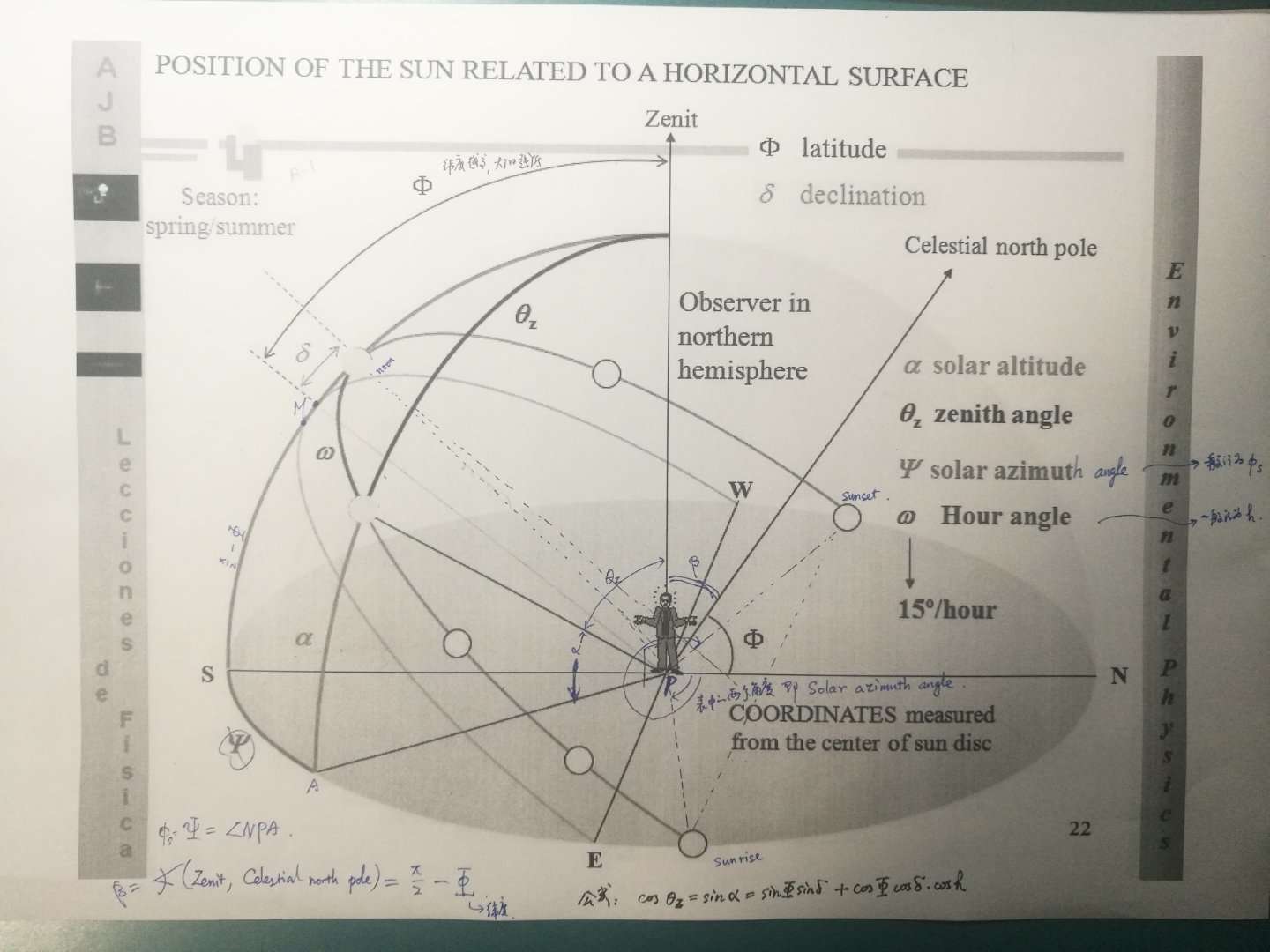
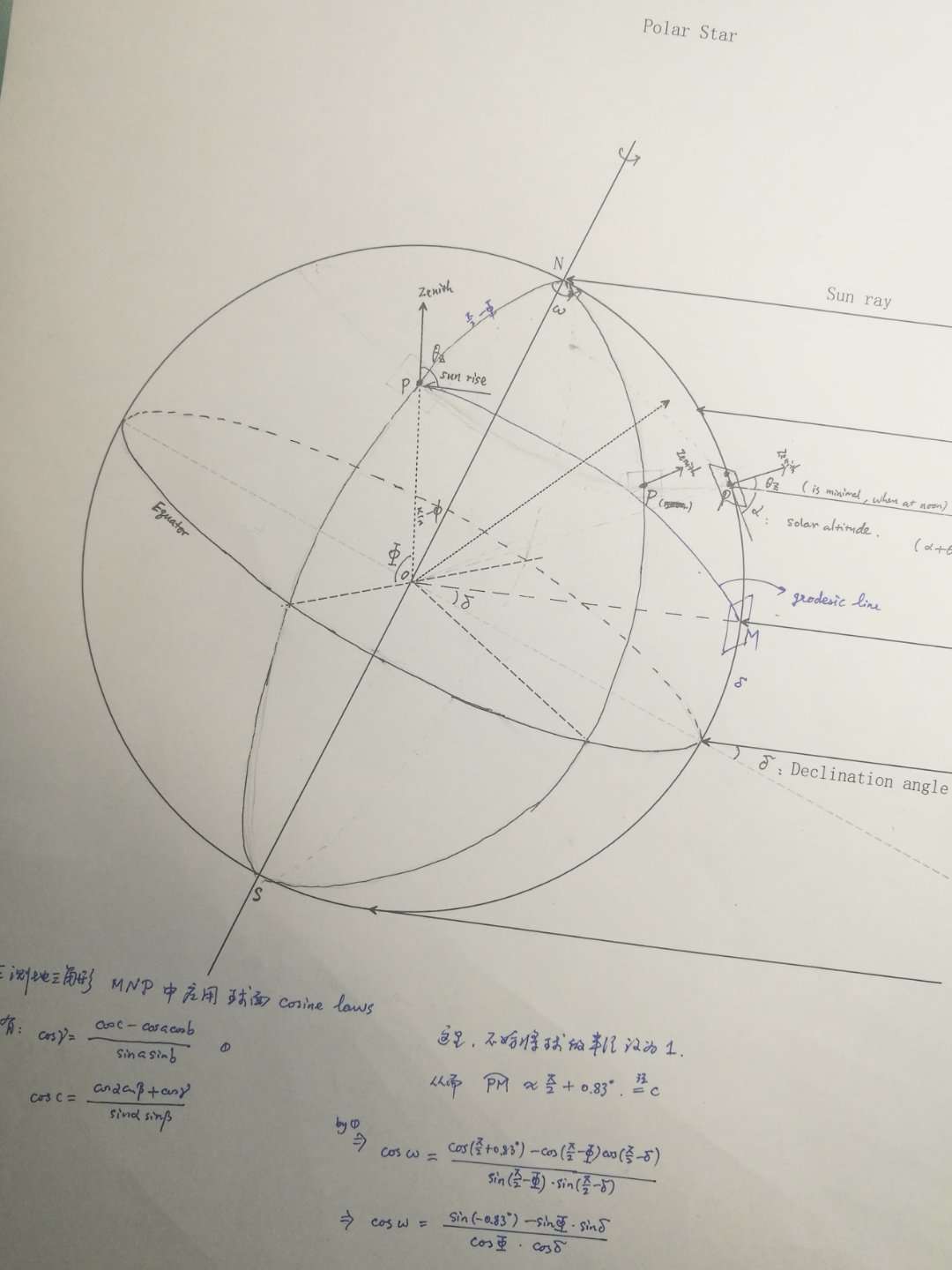
Posted by haifeng on 2019-02-14 10:40:17 last update 2019-02-14 10:50:16 | Answers (0) | 收藏


Posted by haifeng on 2014-10-26 12:52:12 last update 2014-10-26 12:59:00 | Answers (0) | 收藏
在 $\mathbb{R}^{n+1}$ 中, 考虑球面 $S^n(r)$, 它上面的点 $(x_1,x_2,\ldots,x_{n+1})$ 满足方程
\[
x_1^2+x_2^2+\cdots+x_{n+1}^2=r^2.
\]
取球面坐标:
\[
\begin{cases}
x_1&=r\cos\theta_1,\\
x_2&=r\sin\theta_1\cos\theta_2,\\
&\vdots\\
x_i&=r\sin\theta_1\sin\theta_2\cdots\sin\theta_{i-1}\cos\theta_i,\\
x_{i+1}&=r\sin\theta_1\sin\theta_2\cdots\sin\theta_{i-1}\sin\theta_{i}\cos\theta_{i+1},\\
x_{i+2}&=r\sin\theta_1\sin\theta_2\cdots\sin\theta_{i}\sin\theta_{i+1}\cos\theta_{i+2},\\
&\vdots\\
x_n&=r\sin\theta_1\sin\theta_2\cdots\sin\theta_{n-1}\cos\theta_n,\\
x_{n+1}&=r\sin\theta_1\sin\theta_2\cdots\sin\theta_{n-1}\sin\theta_n.\\
\end{cases}
\]
证明 $S^n(r)$ 上的体积形式为
\[
r^n\sin^{n-1}\theta_1\sin^{n-2}\theta_2\cdots\sin^2\theta_{n-2}\sin\theta_{n-1}d\theta_1\theta_2\cdots\theta_n.
\]
Posted by haifeng on 2014-10-23 15:45:07 last update 2014-10-23 16:05:17 | Answers (2) | 收藏
\[
\cos a=\cos b\cos c+\sin b\sin c\cos\alpha.
\]
若 $a$ 很小, 则 $\cos a\approx 1-\frac{a^2}{2}$. 因此, 当 $a,b,c\rightarrow 0$ 时, 球面的第一余弦定律转化为欧氏空间的余弦定律.
注: 此定律有两种证明方法.
Posted by haifeng on 2014-10-19 17:44:43 last update 2014-10-19 17:54:26 | Answers (1) | 收藏
(i) 若 $\triangle A'B'C'$ 是 $\triangle ABC$ 的极三角形, 则 $\triangle ABC$ 是 $\triangle A'B'C'$ 的极三角形.
(ii) 若 $\alpha,\beta,\gamma$ 是 $\triangle ABC$ 的三个角, $aR,bR,cR$ 分别是它三边的长度 ($R$ 是球面的半径), 则极三角形 $\triangle A'B'C'$ 的三个角是 $\pi-a$, $\pi-b$, $\pi-c$, 三边长度为 $(\pi-\alpha)R$, $(\pi-\beta)R$, $(\pi-\gamma)R$.