求定积分 $\int_0^1\frac{1+\cos\pi t}{1-t^2}\mathrm{d}t$.

可以使用复变函数中的围道积分.

这个反常积分 $\displaystyle\int_0^{\infty}\frac{1-\cos x}{x^2}\mathrm{d}x$ 是复分析中的一个经典例子. 

思路是考虑复函数 $f(z)=\dfrac{1-e^{iz}}{z^2}$, 这里 $z\in\mathbb{C}$. $z=0$ 是复函数 $f(z)$ 的二重极点. 在构造环路（围道）积分时, 需避开此极点（一般用半径极小的圆周的一段来避开, 这样是为了好计算）, 同时需要将原积分跟此环路中的某一段积分联系在一起, 且其余段的积分也相对容易计算才行.

[思考] 为何不考虑 $f(z)=\dfrac{1-\cos z}{z^2}$ ?

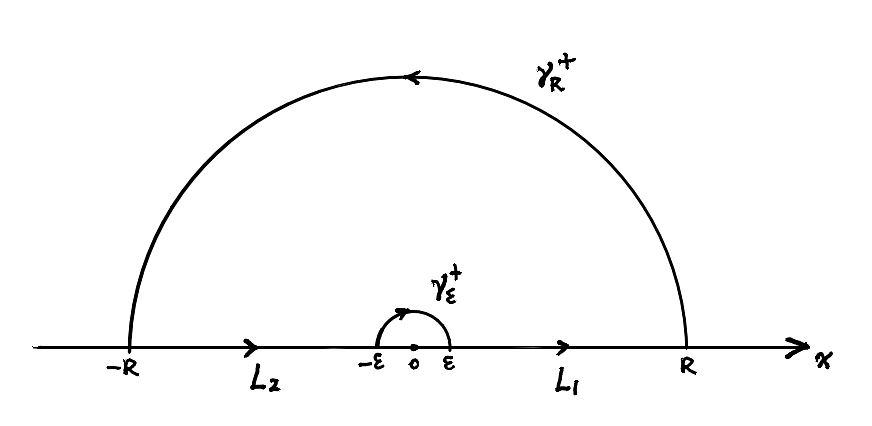
若记 $B_{\varepsilon}(0)$ 为以原点为中心半径为 $\varepsilon$ 的开圆盘, 则取 $\gamma_{\varepsilon}^+$ 为 $B_{\varepsilon}(0)$ 上半部分边界, 方向为从 $(-\varepsilon,0)$ 到 $(\varepsilon,0)$. $L_1$ 为从 $(\varepsilon,0)$ 到 $(R,0)$ 的有向线段,  $\gamma_{R}^+$ 为 $B_{R}(0)$ 上半部分边界, 方向为从 $(R,0)$ 到 $(-R,0)$. $L_2$ 为从 $(-R,0)$ 到 $(-\varepsilon,0)$ 的有向线段. 这四段曲线首尾相接, 构成一个闭回路, 记为 $\Gamma_{\varepsilon}$. 即

\[\Gamma_{\varepsilon}=\gamma_{\varepsilon}^{+} + L_1+\gamma_{R}^{+}+L_2.\]

这里路径上的 $+$ 号指取的是正向. $\Gamma_{\varepsilon}$ 所围的闭区域记为 $\Omega_{\varepsilon}$, 则函数 $\dfrac{1-\cos z}{z^2}$ 在 $\Omega_{\varepsilon}$ 上是解析的. 于是

\[
\int_{\Gamma_{\varepsilon}}\frac{1-e^{iz}}{z^2}\mathrm{d}z=0.
\]

这推出

\[
\int_{L_1}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{\gamma_{R}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{L_2}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{\gamma_{\varepsilon}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z=0.\tag{*}
\]

由于在 $\gamma_{R}^{+}$ 上, $\biggl|\frac{1-e^{iz}}{z^2}\biggr|=\frac{|1-e^{iz}|}{R^2}\leqslant\frac{2}{R^2}$, 因此

\[
\biggl|\int_{\gamma_{R}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z\biggr|=\left|\int_{\gamma_R}\frac{1-e^{iz}}{z^2}\cdot\vec{\tau}\mathrm{d}s\right|\leqslant\int_{\gamma_{R}}\biggl|\frac{1-e^{iz}}{z^2}\biggr|\mathrm{d}s\leqslant\frac{2}{R^2}\cdot\pi R\rightarrow 0,\quad\text{当}\ R\rightarrow\infty.
\]

这里 $\gamma_{R}$ 就是指中心在原点、半径为 $R$ 的(无方向的)上半圆周, $\vec{\tau}$ 是曲线 $\gamma_{R}$ 上的单位切向量. 这里用到了第二类型曲线积分和第一类型曲线积分之间的关系.

\[
e^{iz}=1+\frac{iz}{1!}+\frac{(iz)^2}{2!}+\frac{(iz)^3}{3!}+\cdots
\]

故

\[
\begin{split}
\frac{1-e^{iz}}{z^2}&=-\frac{iz}{z^2}-\frac{1}{z^2}(\frac{(iz)^2}{2!}+\frac{(iz)^3}{3!}+\cdots)\\
&=-\frac{i}{z}+(\frac{1}{2!}+\frac{iz}{3!}-\frac{z^2}{4!}-\frac{iz^3}{5!}+\cdots)\\
&=-\frac{i}{z}+E(z),
\end{split}
\]

这里 $E(z)=\frac{1}{2!}+\frac{iz}{3!}-\frac{z^2}{4!}-\frac{iz^3}{5!}+\cdots$ 当 $z\rightarrow 0$ 是有界的. 故

\[
\int_{\gamma_{\varepsilon}^{+}}E(z)\mathrm{d}z\rightarrow 0,\quad\text{当}\ \varepsilon\rightarrow 0.
\]

而

\[
\int_{\gamma_{\varepsilon}^{+}}\frac{-i}{z}\mathrm{d}z=\int_{\pi}^{0}\frac{-i}{\varepsilon e^{i\theta}}\cdot ie^{i\theta}\mathrm{d}\theta=\int_{\pi}^{0}(-i^2)\mathrm{d}\theta=-\pi.
\]

故

\[
\int_{\gamma_{\varepsilon}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z=\int_{\gamma_{\varepsilon}^{+}}\frac{-i}{z}\mathrm{d}z+\int_{\gamma_{\varepsilon}^{+}}E(z)\mathrm{d}z\rightarrow -\pi,\quad\text{当}\ \varepsilon\rightarrow 0.
\]

另一方面,

\[
\begin{split}
\int_{L_1}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{L_2}\frac{1-e^{iz}}{z^2}\mathrm{d}z&=\int_{\varepsilon}^{R}\frac{1-e^{ix}}{x^2}\mathrm{d}x+\int_{-R}^{-\varepsilon}\frac{1-e^{ix}}{x^2}\mathrm{d}x\\
&\stackrel{t=-x}{=}\int_{\varepsilon}^{R}\frac{1-e^{ix}}{x^2}\mathrm{d}x+\int_{R}^{\varepsilon}\frac{1-e^{-it}}{t^2}\cdot(-1)\mathrm{d}t\\
&=\int_{\varepsilon}^{R}\frac{1-e^{ix}}{x^2}\mathrm{d}x+\int_{\varepsilon}^{R}\frac{1-e^{-ix}}{x^2}\mathrm{d}x\\
&=\int_{\varepsilon}^{R}\frac{2-(e^{ix}+e^{-ix})}{x^2}\mathrm{d}x\\
&=2\int_{\varepsilon}^{R}\frac{1-\cos x}{x^2}\mathrm{d}x
\end{split}
\]

最后, 在 $(*)$ 式中令 $R\rightarrow\infty$, $\varepsilon\rightarrow 0$, 得

\[
2\int_{0}^{+\infty}\frac{1-\cos x}{x^2}\mathrm{d}x+(-\pi)=0,
\]

即有

\[
\int_{0}^{+\infty}\frac{1-\cos x}{x^2}\mathrm{d}x=\frac{\pi}{2}.
\]

参考 [1] P.44 Example 2.

[1] Elias M. Stein & Rami Shakarchi,  Complex Analysis.

施瓦茨导数(Schwarzian derivative)

对于解析函数 $f(z)$, 称下面的表达式

\[
\{f,z\}:=\frac{f'''(z)}{f'(z)}-\frac{3}{2}\biggl(\frac{f''(z)}{f'(z)}\biggr)^2
\]

为施瓦茨导数(Schwarzian derivative). 

由于

\[
\biggl(\frac{f''(z)}{f'(z)}\biggr)'=\frac{f'''(z)f'(z)-f''(z)f''(z)}{(f'(z))^2}=\frac{f'''(z)}{f'(z)}-\biggl(\frac{f''(z)}{f'(z)}\biggr)^2,
\]

施瓦茨导数 $\{f,z\}$ 又可写为

\[
\{f,z\}=\biggl(\frac{f''(z)}{f'(z)}\biggr)'-\frac{1}{2}\biggl(\frac{f''(z)}{f'(z)}\biggr)^2.
\]

若令

\[
g(z)=\frac{af(z)+b}{cf(z)+d},
\]

则有

\[
\frac{g'''(z)}{g'(z)}-\frac{3}{2}\biggl(\frac{g''(z)}{g'(z)}\biggr)^2=\frac{f'''(z)}{f'(z)}-\frac{3}{2}\biggl(\frac{f''(z)}{f'(z)}\biggr)^2.
\]

即 $\{g,z\}=\{f,z\}$, 即得到如下命题.

命题.  施瓦茨导数(Schwarzian derivative)在莫比乌斯变换下不变.

对于解析函数 $f(z)$, 若 $s$ 是另一参数, 则根据 M. Barner, 可证明

\[
\{f,t\}=\varphi^{-2}\cdot\Bigl(\{f,z\}+2A^2-2A'\Bigr)
\]

这里 $\varphi=\frac{\mathrm{d}t}{\mathrm{d}z}$, $A=\frac{1}{2}\frac{\varphi'}{\varphi}$.

References:

[1] Schwarzian derivative - Encyclopedia of Mathematics

这里首先复习一下 $e^z$ 的定义. 当 $z$ 取复数时, 模仿实变量函数 $e^x$ 的定义, 将 $e^z$ 定义为

\[
e^z=1+\frac{z^1}{1!}+\frac{z^2}{2!}+\frac{z^3}{3!}+\cdots+\frac{z^n}{n!}+\cdots
\]

类似地, 定义 $\sin z$ 和 $\cos z$ 如下:

\[
\sin z=z-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+\cdots
\]

\[
\cos z=1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\cdots
\]

于是, 易得

\[
e^{iz}=\cos z+i\sin z\tag{1}
\]

对 $z\in\mathbb{C}$ 也成立.

令 $z$ 为 $-z$, 根据上面 $\sin z$ 和 $\cos z$ 的定义, 有

\[
e^{-iz}=\cos z-i\sin z.\tag{2}
\]

(1) 和 (2) 相乘, 得

\[
1=e^{iz}\cdot e^{-iz}=\cos^2 z+\sin^2 z.
\]

因此 $\sin ^2 z+\cos^2 z=1$ 对 $z\in\mathbb{C}$ 也成立.

最后, 由于 $e^z$ 可以是无界的, 故 $\sin z$ 和 $\cos z$ 也是无界的.

全纯的定义

Cauchy 积分公式  ==>  全纯函数的均值性质  ==> 最大模原理  ==> Schwarz 引理

Cauchy 积分公式

\[
f(z)=\frac{1}{2\pi i}\int_{\partial D(z_0, r)}\frac{f(\zeta)}{\zeta-z_0}\mathrm{d}\zeta
\]

全纯函数的均值性质,  指的是全纯函数 $f(z)$ 在某点 $z_0$ 处的值等于 $f(z)$ 在以 $z_0$ 为中心的一个圆上的值的平均.

具体的,

\[
f(z)=\frac{1}{2\pi}\int_{0}^{2\pi}f(z_0+re^{i\theta})\mathrm{d}\theta
\]

设 $R > 0$, 定义 $\varphi:\ \mathbb{C}\rightarrow\mathbb{C}$ 为

\[
\varphi(z)=\begin{cases}
z, & |z|\leqslant R,\\
\frac{Rz}{|z|}, & |z| > R,
\end{cases}
\]

证明 $\varphi$ 是复平面到半径为 $R$ 的圆盘上的连续映射.

注:  这个函数用在 Lusin 定理的证明中. Lusin 定理先就实的有界函数进行证明, 对于复函数, 要用到这里的 $\varphi$.

设 $T > 0$, $\omega\in\mathbb{R}$. 定义

\[
f(s)=\int_{0}^{T}(e^{i\omega t-its}-e^{i\omega t+its})\mathrm{d}t,
\]

这里 $i=\sqrt{-1}$.

求这样的 $s$, 它对任意 $(T,\omega)\in\mathbb{R}^{+}\times\mathbb{R}$, 都有 $f(s)=0$.

Remark:

题目来源于浙江大学某老师布置的题目.

定义: 一个双周期函数如果是半纯的(也称“亚纯”,  即在有限复平面上仅有的奇点是极点), 就称为椭圆函数.

References:

潘承洞、潘承彪 著《模形式导引》  北京大学出版社.

复变函数 $\mathrm{Ln}z$ 或 $\mathrm{Log}z$ 的定义.

和实函数 $y=\ln x$ 的定义类似, 若复数 $\omega$ 满足 $e^{\omega}=z$, 则定义 $\mathrm{Ln}z=\omega$. 

由于

\[
e^{\omega+i2k\pi}=e^{\omega}.
\]

因此, $f(z)=\mathrm{Ln}z$ 是一个多值函数.  设 $z=re^{i\theta}$,  $\omega=u+iv$, $u,v$ 是实数. 则

\[
z=e^{\omega}=e^{u+iv}=e^u\cdot e^{iv}=e^u(\cos v+i\sin v)
\]

于是 $r=e^u$, 从而 $u=\ln r=\ln|z|$. $v=\theta+2k\pi$, $k$ 是任意整数. 

\[
f(z)=\mathrm{Ln}z=u+iv=\ln r+i(\theta+2k\pi)
\]

如果仅考虑 $k=0$, $\theta=\arctan\frac{y}{x}$, 这里 $x=r\cos\theta$, $y=r\sin\theta$, 则称这样的 $\mathrm{Ln}z$ 函数是其中的一个(主)分支.

验证: $\mathrm{Ln}z$ 在任一分支上满足柯西-黎曼方程(Cauchy-Riemann equation), 从而 $\mathrm{Ln}z$ 在分支上是全纯函数.

由于满足柯西-黎曼方程是复变函数 $f(z)$ 可导(即全纯)的充要条件, 故

\[
\frac{\mathrm{d}}{\mathrm{d}z}f(z)=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}.
\]

或简记为 $f'(z)=u_x+iv_x$.

Claim.

\[
\frac{\mathrm{d}}{\mathrm{d}z}\mathrm{Ln}z=\frac{1}{z}
\]

参考自 [1] 第二卷 第九章 复变函数.

References:

[1]  A. D. 亚历山大洛夫  等 著 《数学，它的内容、方法和意义》,  科学出版社

令 $z=re^{i\theta}$, 写出 $\frac{e^{it}+z}{e^{it}-z}$ 的实部和虚部

\[
\mathrm{Re}(\frac{e^{it}+z}{e^{it}-z})=\frac{1-r^2}{1-2r\cos(\theta-t)+r^2},
\]

\[
\mathrm{Im}(\frac{e^{it}+z}{e^{it}-z})=\frac{2r\sin(\theta-t)}{1-2r\cos(\theta-t)+r^2}.
\]

若令 $r\in[0,1)$, 则 $\mathrm{Re}(\frac{e^{it}+z}{e^{it}-z}) > 0$. 我们记 $P_r(\theta-t)=\mathrm{Re}(\frac{e^{it}+z}{e^{it}-z})$.

References:

W. Rudin, 《实分析和复分析》