一维装球问题(one-dimensional circle packing problem)
一维装球问题:
有 $N$ 个半径分别是 $r_1,r_2,\ldots,r_N$ 的圆盘(比如光盘). 将这些圆盘装到一个盒子中使得每个圆盘都与盒子的底边相切. 任何两个圆盘至多有一个公共点.
问这个盒子的底边长度最小是多少?
假设底边最短长是 $f(r_1,r_2,\ldots,r_N)$.
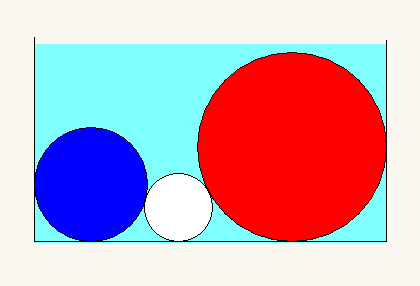
记 $h(x,y)=2\sqrt{xy}$.
Exer. 不妨假设 $r_1\leqslant r_2\leqslant r_3$. 记
\[
d=\max\{h(r_1,r_2)+h(r_1,r_3),\ h(r_2,r_3)\},
\]
证明
\[
f(r_1,r_2,r_3)=\max\{r_2+d, r_3\}+r_3.
\]
Q. $f(r_1,r_2,r_3,r_4)=?$
如果圆盘的排放是按原有顺序的, 若记 $\varphi_n(r_1,r_2,\ldots,r_n)$ 为排放这 $n$ 个圆盘的盒子底边的最短长度, 对于依次输入的 $r_1,r_2,\ldots,r_k$, 请编程依次输出 $\varphi_k$ 值.
References:
Mark Allen Weiss, Data Structures and Algorithm Analysis in C++, Third Edition.
张怀勇 等译. Ex. 10.46, P.348
相关问题: