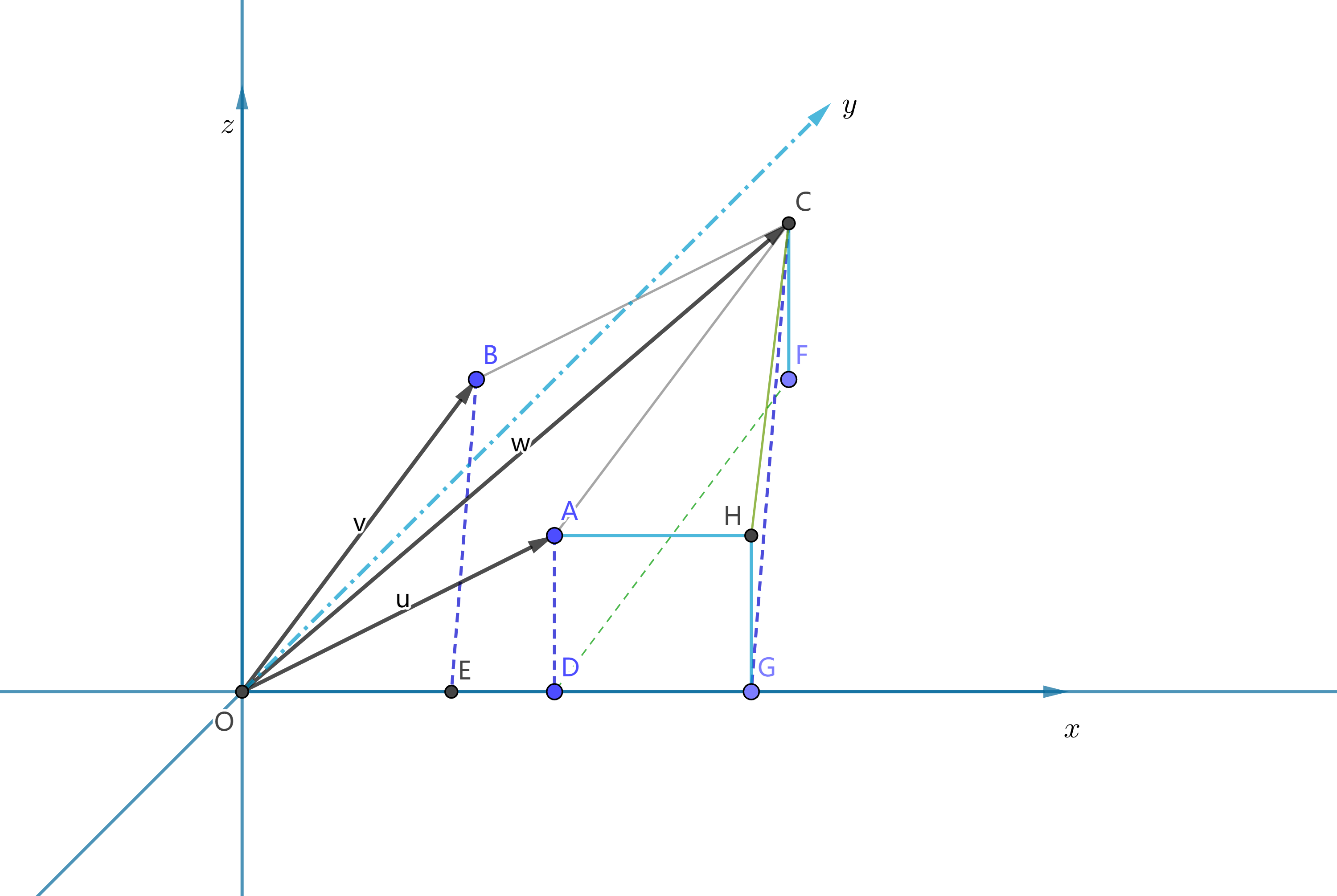
设 $\vec{a},\vec{b},\vec{c}\in\mathbb{R}^3$, 证明:
\[\mathrm{Prj}_{\vec{a}}(\vec{b}+\vec{c})=\mathrm{Prj}_{\vec{a}}(\vec{b})+\mathrm{Prj}_{\vec{a}}(\vec{c}).\]
这里 $\mathrm{Prj}_{\vec{a}}(\vec{b})$ 表示向量 $\vec{b}$ 在 $\vec{a}$ 上的投影.
1
不妨记 $\vec{u}=\vec{b}$, $\vec{v}=\vec{c}$
将 $\vec{u}$ 和 $\vec{v}$ 起始点作为原点, 以 $\vec{a}$ 所在的轴作为 $x$ 轴, $x$ 轴正向与 $\vec{a}$ 一致, 建立直角坐标系, 如图. $\vec{u}=\overrightarrow{OA}$, $\vec{v}=\overrightarrow{OB}$, 则 $\overrightarrow{OC}=\vec{u}+\vec{v}$.
过 $A$, $B$, $C$ 作 $x$ 轴的垂线, 垂足分别为 $D$, $E$, $F$. 则
\[
x_D=\text{Prj}_{\vec{a}}\vec{u},\quad x_E=\text{Prj}_{\vec{a}}\vec{v},\quad x_G=\text{Prj}_{\vec{a}}(\vec{u}+\vec{v}).
\]
于是即要证明 $x_G=x_D+x_E$.
$CG$, $HG$ 都垂直于 $x$ 轴, 故 $x$ 轴垂直 $CH$. 而 $AH$ 与 $x$ 轴平行, 故 $AH\perp CH$.
容易证明 $\text{Rt}\triangle OEB$ 和 $\text{Rt}\triangle AHC$ 全等, 因为 $|OB|=|AC|$, 且 $\angle BOE=\angle CAH$.
因此, $|OE|=|AH|$. 而 $|AH|=|DG|$, 故 $|OE|=|DG|$. 证毕.