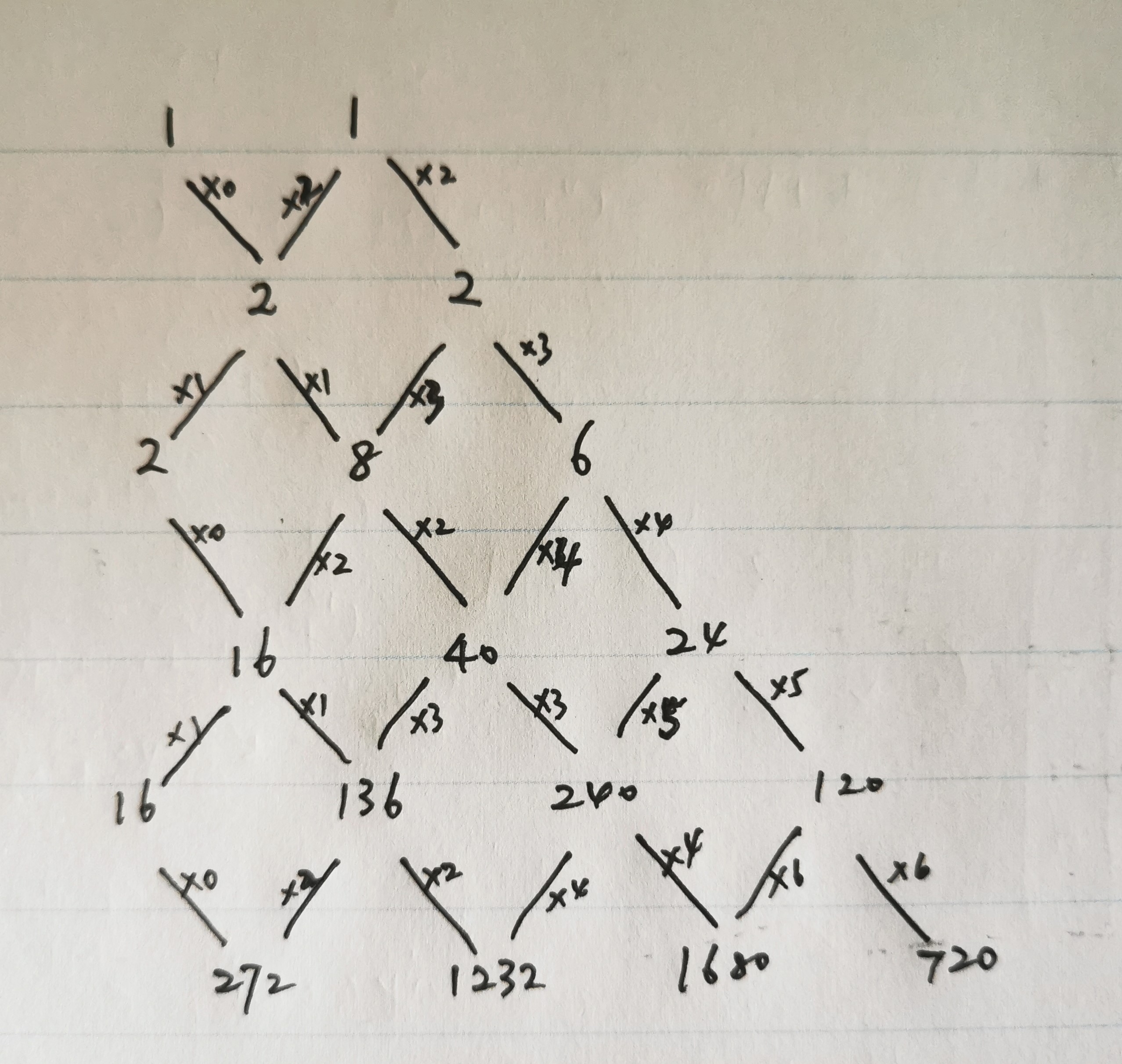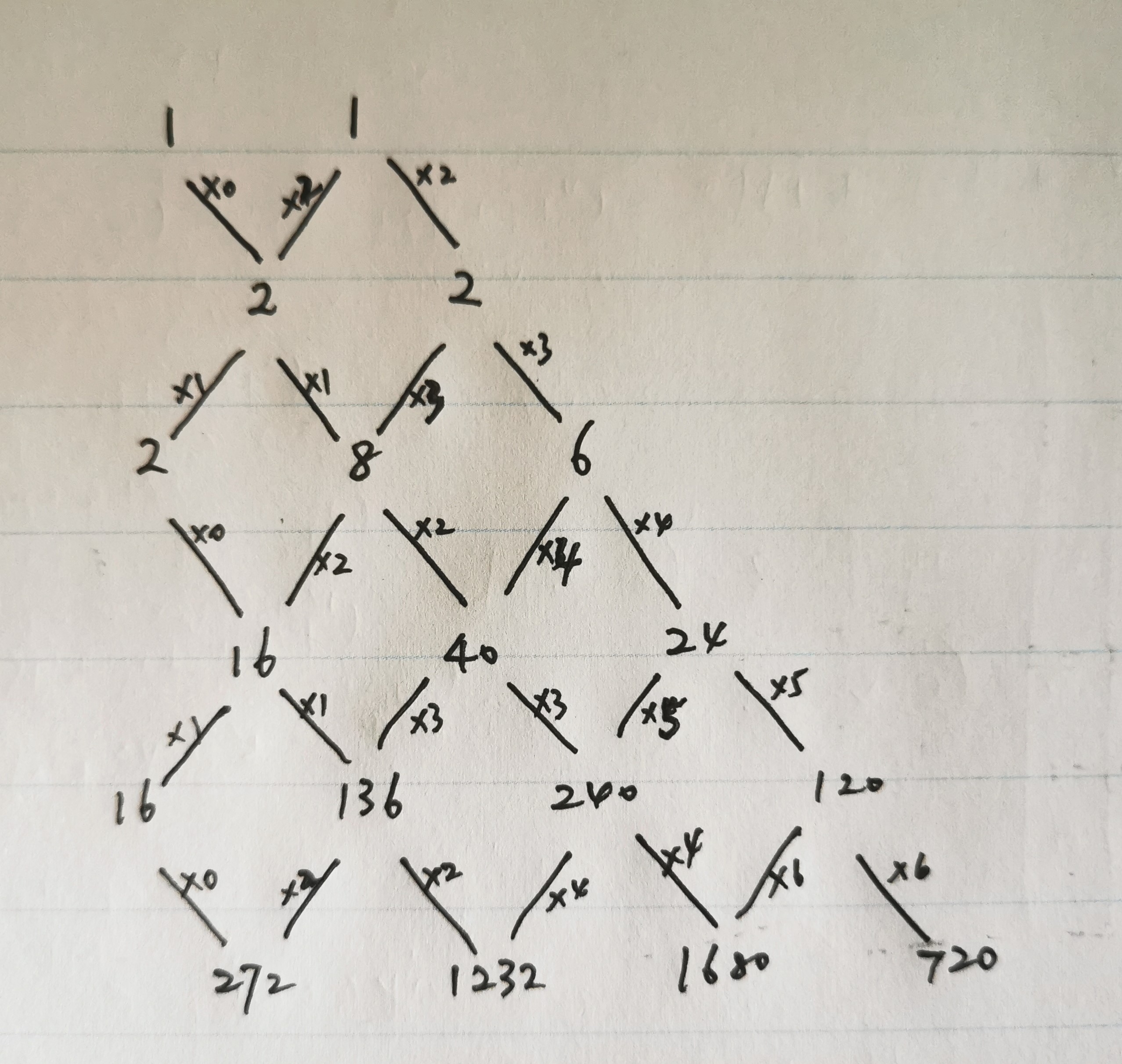问题及解答

$y=\tan x$ 的高阶导数都可以表示为 $\tan x$ 的多项式.

证明: $(\tan x)^{(n)}$ 中最高次 $\tan^{n+1}x$ 前面得系数是 $n!$.

例如:

\[y'=(\tan x)'=\sec^2 x=1+\tan^2 x\]

\[
\begin{split}
y''=(\sec^2 x)'&=2\sec x\cdot(\sec x)'=2\sec x\cdot\sec x\tan x\\
&=2\sec^2 x\tan x=2(1+\tan^2 x)\tan x\\
&=2\tan^3 x+2\tan x=2\tan x\cdot(1+\tan^2 x)
\end{split}
\]

求 $y^{(n)}(0)$

[Hint] 利用 $y'=(\tan x)'=\sec^2 x=\frac{1}{\cos^2 x}$ 得 $y'\cdot\cos^2 x=1$. 然后两边再求 $n$ 阶导数, 利用 Leibniz 求导法则.

\[
\begin{split}
y'''=(\tan x)'''&=(2\tan x\cdot(1+\tan^2 x))'\\
&=2\sec^2 x\cdot (1+\tan^2 x)+2\tan x\cdot 2\tan x\cdot\sec^2 x\\
&=2\sec^2 x\cdot (1+3\tan^2 x)\\
&=2(1+\tan^2 x)(1+3\tan ^2 x)
\end{split}
\]

\[
\begin{split}
y^{(4)}=(\tan x)^{(4)}&=\bigl(2(1+\tan^2 x)(1+3\tan ^2 x)\bigr)'\\
&=\bigl(2(1+4\tan^2 x+3\tan^4 x)\bigr)'\\
&=2\cdot(4\cdot 2\tan x\cdot\sec^2 x+3\cdot 4\tan^3 x\cdot\sec^2 x)\\
&=8\tan x\cdot\sec^2 x\cdot(2+3\tan^2 x)\\
&=8\tan x\cdot(1+\tan^2 x)\cdot(2+3\tan^2 x)
\end{split}
\]

使用归纳法, 容易证明 $(\tan x)^{(n)}$ 是关于 $\tan x$ 的多项式.

\[
\begin{split}
y^{(5)}=(\tan x)^{(5)}&=\big(8\tan x\cdot(1+\tan^2 x)\cdot(2+3\tan^2 x)\big)'\\
&=\big(8\tan x\cdot(2+5\tan^2 x+3\tan^4 x)\big)'\\
&=8\sec^2 x\cdot(2+5\tan^2 x+3\tan^4 x)+8\tan x\cdot(5\cdot 2\tan x\cdot\sec^2 x+3\cdot 4\tan^3 x\cdot\sec^2 x)\\
&=8\sec^2 x\cdot\bigl(2+5\tan^2 x+3\tan^4 x+\tan x\cdot(10\tan x+12\tan^3 x)\bigr)\\
&=8(1+\tan^2 x)\cdot(2+15\tan^2 x+15\tan^4 x)\\
&=16+136\tan^2 x+240\tan^4 x+120\tan^6 x
\end{split}
\]

如果用 $t$ 代表 $\tan x$, 则 $t'=1+t^2$.

\[
\begin{aligned}
y'&=1+t^2\\
y''&=2t(1+t^2)=2t+2t^3\\
y'''&=2(1+t^2)(1+3t^2)=2+8t^2+6t^4\\
y^{(4)}&=8t(1+t^2)(2+3t^2)=16t+40t^3+24t^5\\
y^{(5)}&=8(1+t^2)(2+15t^2+15t^4)=16+136t^2+240t^4+120t^6\\
\end{aligned}
\]

利用归纳法, 可以证明 $y^{(n)}$ 中最高次项 $t^{n+1}$ 前面得系数为 $n!$.

\[
\begin{split}
y^{(6)}&=(16+136t^2+240t^4+120t^6)'_x\\
&=(136\cdot 2t+240\cdot 4t^3+120\cdot 6t^5)\cdot t'\\
&=(272t+960t^3+720t^5)\cdot(1+t^2)\\
&=272t+1232t^3+1680t^5+720t^7
\end{split}
\]

这些数的规律如下,  (发现于2020年10月21日)