$\arctan\frac{1+x}{1-x}$ 与 $\arctan x$ 的关系
证明:
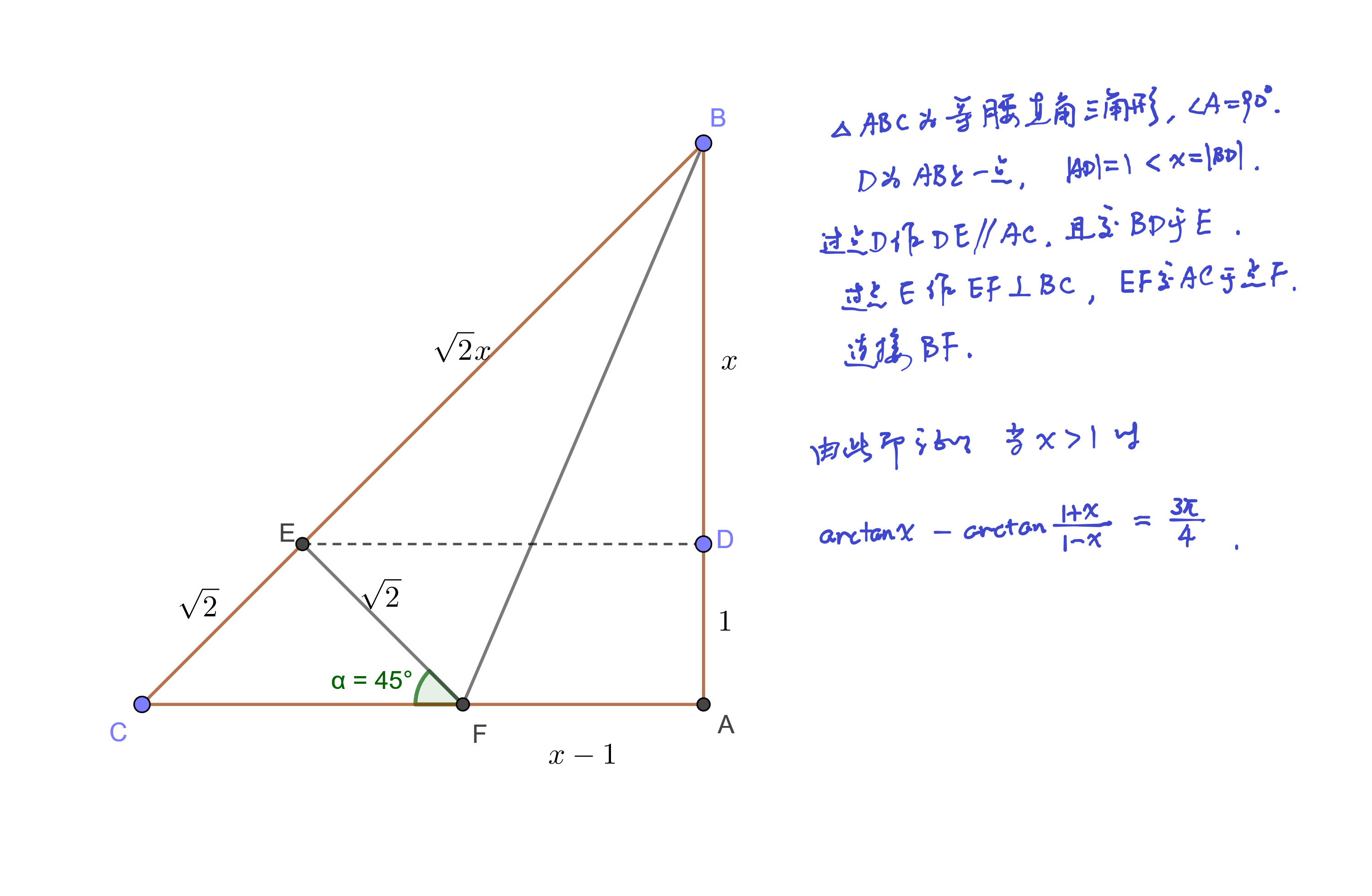
(1) 当 $x > 1$ 时,
\[
\arctan x-\arctan\frac{1+x}{1-x}=\frac{3\pi}{4},
\]
(2) 当 $x < 1$ 时,
\[
\arctan\frac{1+x}{1-x}-\arctan x=\frac{\pi}{4}.
\]
这里还给出了关于(2)的两个几何证明.
证明:
(1) 当 $x > 1$ 时,
\[
\arctan x-\arctan\frac{1+x}{1-x}=\frac{3\pi}{4},
\]
(2) 当 $x < 1$ 时,
\[
\arctan\frac{1+x}{1-x}-\arctan x=\frac{\pi}{4}.
\]
这里还给出了关于(2)的两个几何证明.
1
令 $\alpha=\arctan\frac{1+x}{1-x}$, $\beta=\arctan x$. 则
\[
\begin{split}
\tan(\alpha-\beta)&=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\cdot\tan\beta}\\
&=\frac{\frac{1+x}{1-x}-x}{1+\frac{1+x}{1-x}\cdot x}\\
&=\frac{1+x-x(1-x)}{1-x+x(1+x)}\\
&=\frac{1+x^2}{1+x^2}\\
&=1.
\end{split}
\]
故 $\alpha-\beta=\frac{\pi}{4}+k\pi$, $k$ 是某个整数.
注意到
\[
\frac{1+x}{1-x}-x < 0 \Leftrightarrow \frac{1+x-x(1-x)}{1-x} <0 \Leftrightarrow \frac{1+x^2}{1-x} < 0 \Leftrightarrow 1-x <0
\]
分情况讨论:
(1) $\frac{1+x}{1-x}-x < 0$, 即 $x > 1$ 时.
此时
\[
\frac{1+x}{1-x} < -1
\]
从而
\[
\pi=\frac{\pi}{2}-(-\frac{\pi}{2}) > \arctan x-\arctan\frac{1+x}{1-x} > \frac{\pi}{4}-(-\frac{\pi}{4})=\frac{\pi}{2}
\]
由于 $\beta-\alpha=k\pi-\frac{\pi}{4}$, 故
\[
\frac{\pi}{2} < k\pi-\frac{\pi}{4} < \pi
\]
因此, $k=1$. 即有
\[
\arctan x-\arctan\frac{1+x}{1-x}=\frac{3}{4}\pi
\]
(2) $\frac{1+x}{1-x}-x > 0$, 即 $x < 1$ 时,
此时 $\frac{1+x}{1-x} > 1$. 于是
\[
0 < \arctan\frac{1+x}{1-x}-\arctan x <\frac{\pi}{2}-0=\frac{\pi}{2}
\]
由于 $\alpha-\beta=k\pi+\frac{\pi}{4}$, 故 $k=0$. 即有
\[
\arctan\frac{1+x}{1-x}-\arctan x=\frac{\pi}{4}.
\]
2
几何证明1
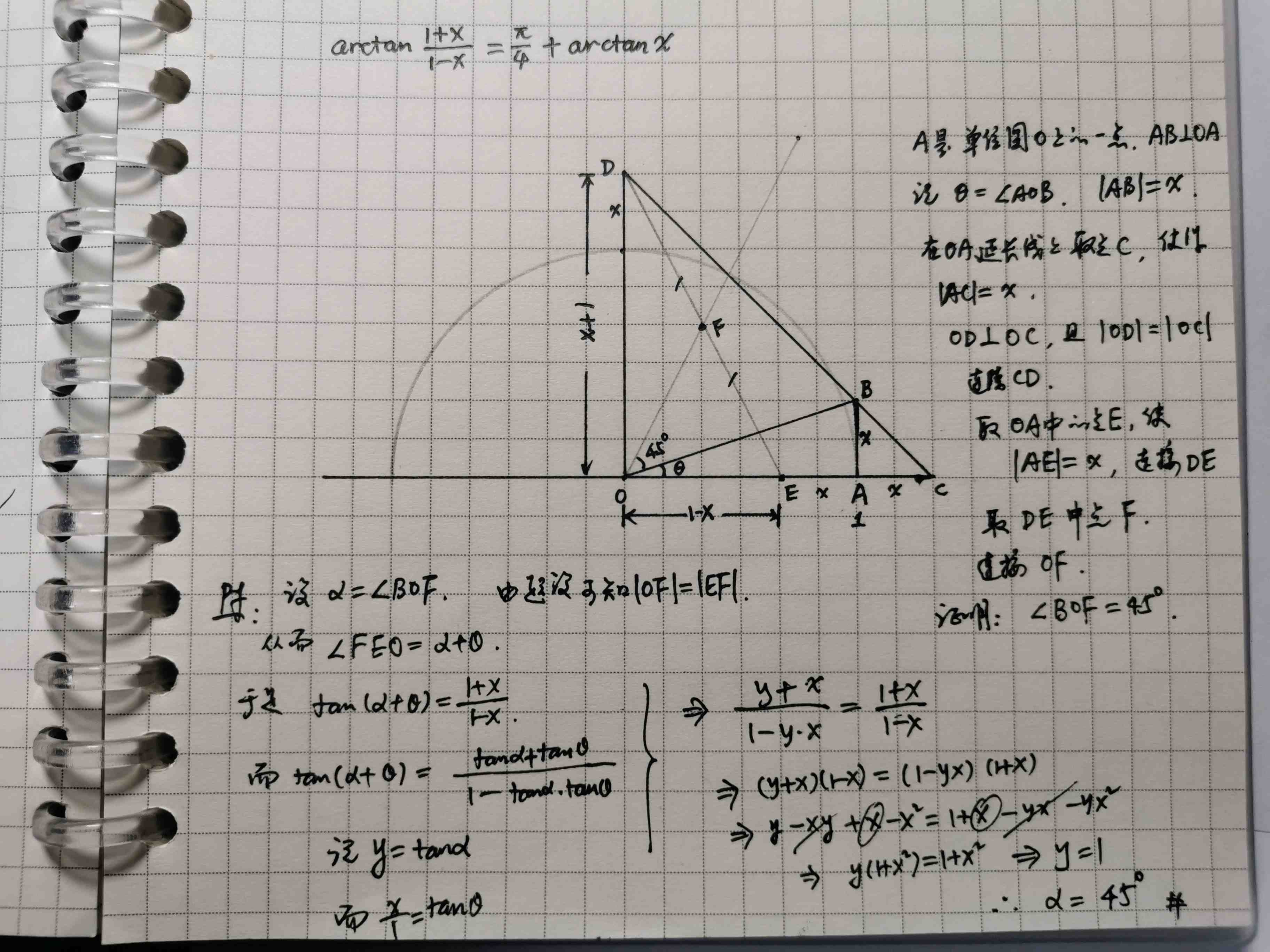
连接 $BF$, 可证明 $BF\perp OF$.
Date: April 26, 2022.
3
几何证明 2. 这个很妙的证明是由张影给出的.

4
根据张影老师的启发, 对于 $x > 1$ 的情形, 可以用下面的几何方法证明.