将0,1,2,...,9这十个数字填到下面的方框中, 使得算式成立.
将0,1,2,...,9这十个数字填到下面的方框中, 使得算式成立.
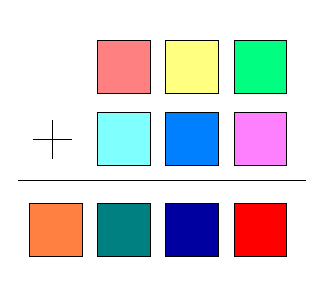
注: 这里我们认为四位数的千位可以是 0.
证明: (1) 四位数的千位只能是 0 或 1;
(2) 0 只能出现在四位数中.
(3) 能否证明四位数的最后一位不是 0?
请编写一个程序, 计算所有可能的解. 并进一步改进你的算法.
将0,1,2,...,9这十个数字填到下面的方框中, 使得算式成立.
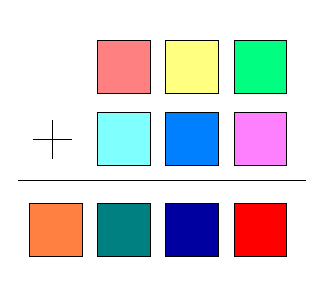
注: 这里我们认为四位数的千位可以是 0.
证明: (1) 四位数的千位只能是 0 或 1;
(2) 0 只能出现在四位数中.
(3) 能否证明四位数的最后一位不是 0?
请编写一个程序, 计算所有可能的解. 并进一步改进你的算法.
1
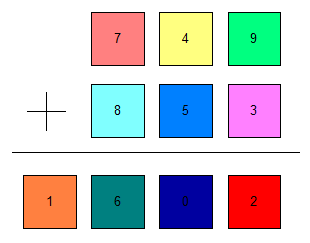
Answer: 如果四位数千位是 1, 则有 96/2=48 个解, 其中 $b=0$ 的有 64/2=32 个解, $c=0$ 的有 32/2=16 个解; 如果四位数千位是 0, 则有 336/2=168 个解; 总共 432/2=216 个解.
(注意: 这里将 749+853=1602 与 853+749=1602 认为是一个解, 因此上面特地写了 /2 .)
我们使用符号来表示各个数字: $xyz+uvw=abcd$, 这里 $xyz, uvw$ 是三位数, $abcd$ 是四位数.
Claim. $a\leqslant 1$.
Pf. 由于两个三位数的百位最多是 9 和 8, 相加等于 17, 所以即使十位上有进位, 也不可能使得 $a=2$.
Claim. 0 只能出现在四位数中.
Pf. 首先 $z,w\neq 0$, 否则 $z,w$ 中的一个会与 $d$ 相等, 与假设不符.
其次 $x,u\neq 0$. 不妨设 $u=0$, 则十位相加必定有进位, 从而 $x+1\equiv b\pmod {10}$. 但此时 $a=1$, 因此表明百位相加有进位, 故 $x=9$, 于是推出 $b=0$. 矛盾.
最后, 不妨假设 $v=0$. 即 $xyz+u0w=1bcd$. 于是个位相加必有进位, 故 $y+1\equiv c\pmod{10}$. 事实上这里 $y\neq 9$, 因此百位上无进位.
从而已经有两个奇数两个偶数($0,1,y,y+1$). 剩余三个奇数三个偶数.
(a) 若 $z,w$ 是两个奇数, 则 $d$ 是偶数, 剩余 $x,u,b$ 中有一奇两偶. 而这是不可能的.
(b) 若 $z,w$ 一奇一偶, 则 $d$ 是奇数, 剩余 $x,u,b$ 中有一奇两偶. 而这是不可能的.
(c) 若 $z,w$ 两个偶数, 则 $d$ 是偶数, 剩余 $x,u,b$ 中有三个奇数, 而这也是不可能的. (注意此时百位上无进位).
因此, 我们证明了 0 必定在 $a,b,c,d$ 中.