问题及解答

设 $ABCD$ 是圆 $O$ 的内接四边形, 四条边的长度分别为 $|AB|=a$, $|BC|=b$, $|CD|=c$, $|DA|=d$. 若 $p$ 是其周长的一半, 即 $p=\frac{1}{2}(a+b+c+d)$, 则 $ABCD$ 的面积为

\[
S=\sqrt{(p-a)(p-b)(p-c)(p-d)}.
\]

证明: 在 $AB$, $BC$, $CD$, $DA$ 上分别取中点 $E, F, G, H$. 易见 $EH\parallel BD$, $FG\parallel BD$ 且 $|EH|=|FG|=\frac{1}{2}|BD|$.  记 $\alpha=\angle BAD$, $\beta=\angle BCD$, 则 $\alpha+\beta=\pi$.

为计算方便, 不妨设 $|AB|=2a$, $|BC|=2b$, $|CD|=2c$, $|DA|=2d$, 此时 $p=a+b+c+d$.

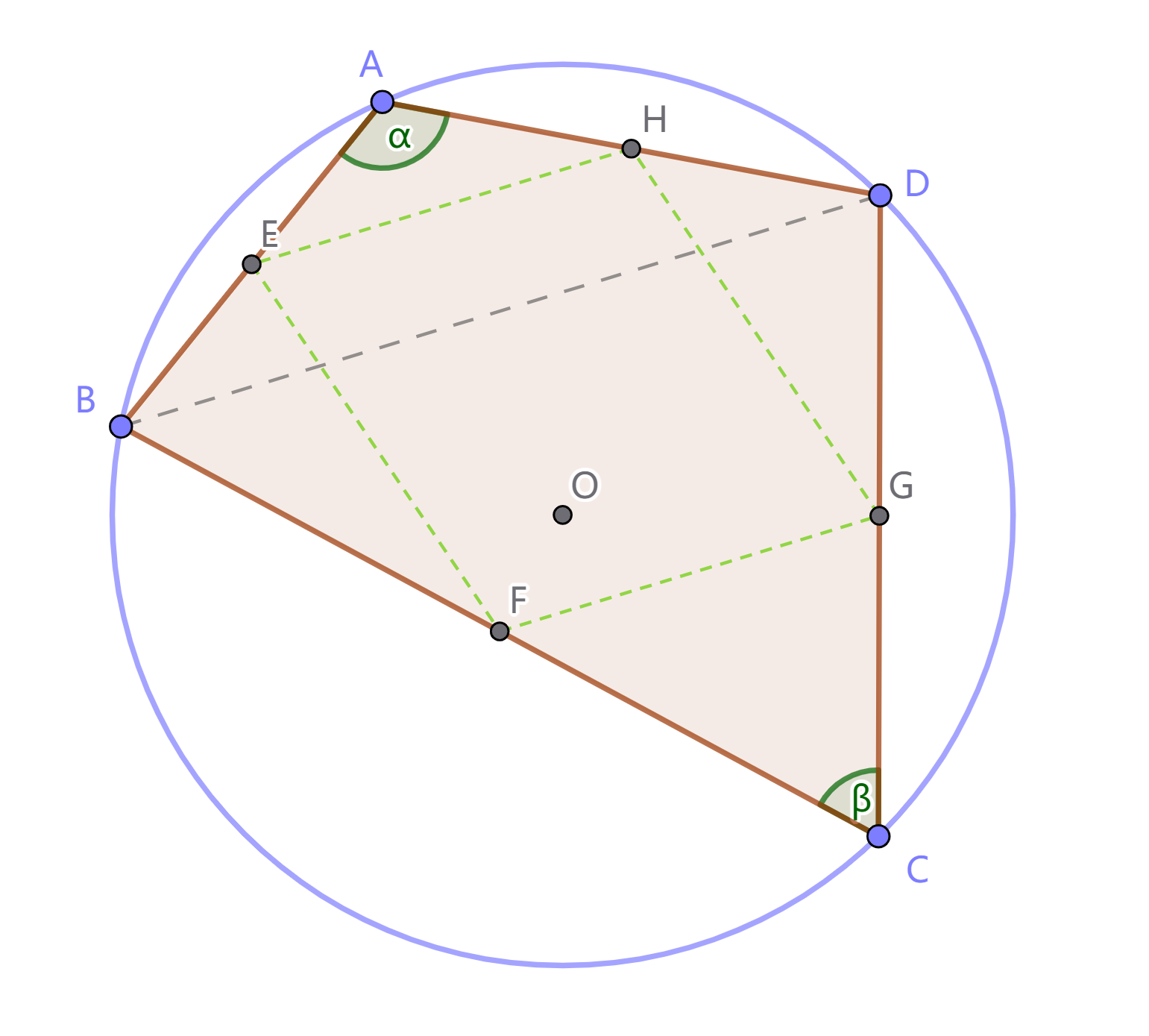
在三角形 $AEH$ 和 $CGF$ 中分别应用余弦定理, 得

\[
a^2+d^2-2ad\cos\alpha=|EH|^2=|FG|^2=b^2+c^2-2bc\cos\beta.
\]

注意到 $\cos\beta=-\cos\alpha$, 故得

\[
a^2+d^2-b^2-c^2=2(ad+bc)\cos\alpha,
\]

即

\[
\cos\alpha=\frac{a^2+d^2-b^2-c^2}{2(ad+bc)}.
\]

四边形 $ABCD$ 的面积

\[
\begin{split}
S_{ABCD}&=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}|AB|\cdot|AD|\cdot\sin\alpha+\frac{1}{2}|BC|\cdot|CD|\cdot\sin\beta\\
&=\frac{1}{2}\cdot 2a\cdot 2d\cdot\sin\alpha+\frac{1}{2}\cdot 2b\cdot 2c\cdot\sin\alpha\\
&=2(ad+bc)\sin\alpha=2(ad+bc)\sqrt{1-\cos^2\alpha}\\
&=2(ad+bc)\sqrt{1-\frac{(a^2+d^2-b^2-c^2)^2}{4(ad+bc)^2}}\\
&=\sqrt{4(ad+bc)^2-(a^2+d^2-b^2-c^2)^2}\ .
\end{split}
\]

另一方面,

\[
\begin{split}
&(p-2a)(p-2b)(p-2c)(p-2d)\\
=&(b+c+d-a)(a+c+d-b)(a+b+d-c)(a+b+c-d)\\
=&[(a+c+d-b)(a+b+d-c)][(b+c+d-a)(a+b+c-d)]\\
=&[(a+d)-(b-c)][(a+d)+(b-c)]\cdot[(b+c)-(a-d)][(b+c)+(a-d)]\\
=&\bigl[(a+d)^2-(b-c)^2\bigr]\cdot\bigl[(b+c)^2-(a-d)^2\bigr]\\
=&\bigl[a^2+d^2-b^2-c^2+2(ad+bc)\bigr]\cdot\bigl[b^2+c^2-a^2-d^2+2(bc+ad)\bigr]\\
=&\Bigl[2(ad+bc)-\bigl(b^2+c^2-a^2-d^2\bigr)\Bigr]\cdot\Bigl[2(ad+bc)+\bigl(b^2+c^2-a^2-d^2\bigr)\Bigr]\\
=&4(ad+bc)^2-(b^2+c^2-a^2-d^2)^2\ .
\end{split}
\]

因此, 

\[
S_{ABCD}=\sqrt{(p-2a)(p-2b)(p-2c)(p-2d)}\ .
\]