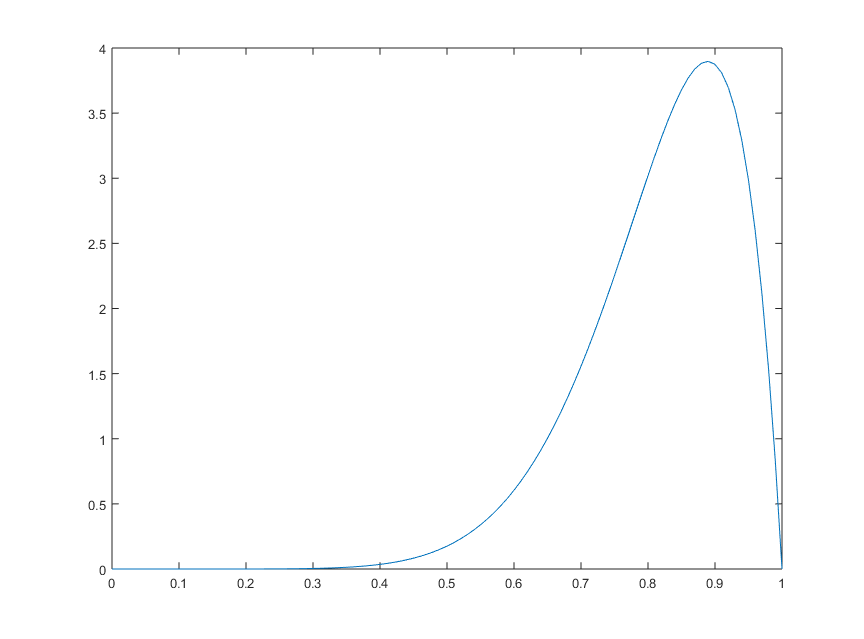
(a) 使用 MATLAB 绘图
>> x=0:0.01:1;
>> y=90*(x.^8).*(1-x);
>> plot(x,y)
cdf
By definition, the cdf is
\[
F(x)=\int_{-\infty}^{x}f(t)dt
\]
Thus, for $x < 0$, $F(x)=0$.
For $x\in[0,1]$, we have
\[
\begin{split}
F(x)&=\int_{0}^{x}90t^8(1-t)dt=90\int_{0}^{x}(t^8-t^9)dt\\
&=90\cdot\Bigl[\frac{1}{9}t^9-\frac{1}{10}t^{10}\Bigr]\biggr|_{0}^{x}\\
&=90\cdot\Bigl[\frac{1}{9}x^9-\frac{1}{10}x^{10}\Bigr]\\
&=10x^9-9x^{10}
\end{split}
\]
For $x > 1$, $F(x)=F(1)=10\cdot 1^9-9\cdot 1^{10}=1$.
That is,
\[
F(x)=\begin{cases}
0, & x\in(-\infty,0),\\
10x^9-9x^{10}, & x\in [0,1],\\
1, & x\in(1,+\infty)
\end{cases}
\]
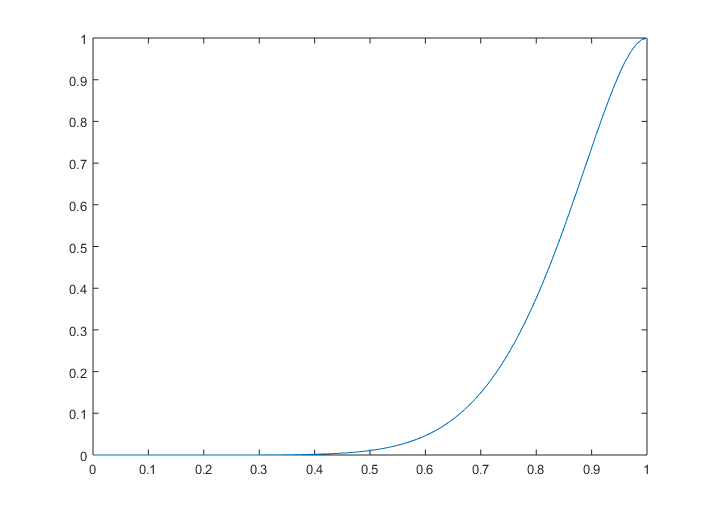
The graph of cdf $F(x)$ is
>> x=0:0.01:1;
>> y=10*x.^9-9*x.^10;
>> plot(x,y)
(b)
\[
P(X\leqslant 0.5)=F(0.5)=10\cdot(\frac{1}{2})^9-9\cdot(\frac{1}{2})^{10}=\frac{2\cdot 10-9}{2^{10}}=\frac{11}{2^{10}}\approx 0.01074219
\]
(c)
\[
\begin{split}
P(.25 < X\leqslant .5)&=P(.25\leqslant X\leqslant .5)\\
&=F(0.5)-F(0.25)\\
&=\Bigl[10\cdot(\frac{1}{2})^9-9\cdot(\frac{1}{2})^{10}\Bigr]-\Bigl[10\cdot(\frac{1}{4})^9-9\cdot(\frac{1}{4})^{10}\Bigr]\\
&\approx 0.0107421875-0.00002956390380859375\\
&=0.01071262359619140625
\end{split}
\]
(d)
Let $p=0.75$, the 75th percentile of the distribution, denoted by $\eta(p)$ is the value which satisfies the equation
\[
0.75=F(\eta(0.75)=\int_{-\infty}^{\eta(0.75)}f(t)dt
\]
If let $x=\eta(0.75)$, then
\[
0.75=F(x)=10x^9-9x^{10}\Rightarrow 9x^{10}-10x^9+\frac{3}{4}=0.
\]
Solve this equation, we get $x\approx 0.9036$
(e)
\[
\begin{split}
\mu=E(X)&=\int_{0}^{1}x\cdot f(x)dx=\int_{0}^{1}x\cdot 90x^8(1-x)dx\\
&=90\cdot\int_{0}^{1}x^9(1-x)dx=90\cdot\int_{0}^{1}(x^9-x^{10})dx\\
&=90\cdot\Bigl[\frac{1}{10}x^{10}-\frac{1}{11}x^{11}\Bigr]\biggr|_{0}^{1}\\
&=90\cdot\Bigl[\frac{1}{10}-\frac{1}{11}\bigr]\\
&=90\cdot\frac{1}{110}=\frac{9}{11}\\
&\approx 0.81818182
\end{split}
\]
\[
\begin{split}
E(X^2)&=\int_{0}^{1}x^2\cdot f(x)dx=\int_{0}^{1}x^2\cdot 90x^8(1-x)dx\\
&=90\cdot\int_{0}^{1}x^{10}(1-x)dx=90\cdot\int_{0}^{1}(x^{10}-x^{11})dx\\
&=90\cdot\Bigl[\frac{1}{11}x^{11}-\frac{1}{12}x^{12}\Bigr]\biggr|_{0}^{1}\\
&=90\cdot\Bigl[\frac{1}{11}-\frac{1}{12}\bigr]\\
&=90\cdot\frac{1}{11\times 12}=\frac{30}{44}\\
&\approx 0.68181818
\end{split}
\]
Thus,
\[
V(X)=E(X^2)-[E(X)]^2\approx 0.68181818-(0.81818182)^2=0.0123966894214876
\]
Therefore,
\[
\sigma_X=\sqrt{V(X)}\approx\sqrt{0.0123966894214876}\approx 0.11134042
\]
(f)
The probability that $X$ is within $1$ standard deviation of its mean value is
\[
\begin{split}
P(|X-\mu| < \sigma_X)&=P(|X-0.81818182| < 0.11134042)=P(0.70684140 < X < 0.92952224)\\
&=F(0.92952224)-F(0.70684140)\\
&=(10*0.92952224^9-9*0.92952224^{10})-(10*0.70684140^9-9*0.70684140^{10})\\
&\approx 0.84658351-0.16025497\\
&=0.68632854
\end{split}
\]

