问题及解答

Suppose the error involved in making a certain measurement is a continuous rv $X$ with pdf
\[
f(x)=
\begin{cases}
  .09375(4-x^2), & -2\leqslant x\leqslant 2, \\
  0, & \mbox{otherwise}.
\end{cases}
\]

• (a) Sketch the graph of $f(x)$.
• (b) Compute $P(X>0)$.
• (c) Compute $P(-1<X<1)$.
• (d) Compute $P(X<-.5\ \text{or}\ X>.5)$.
   

(a)

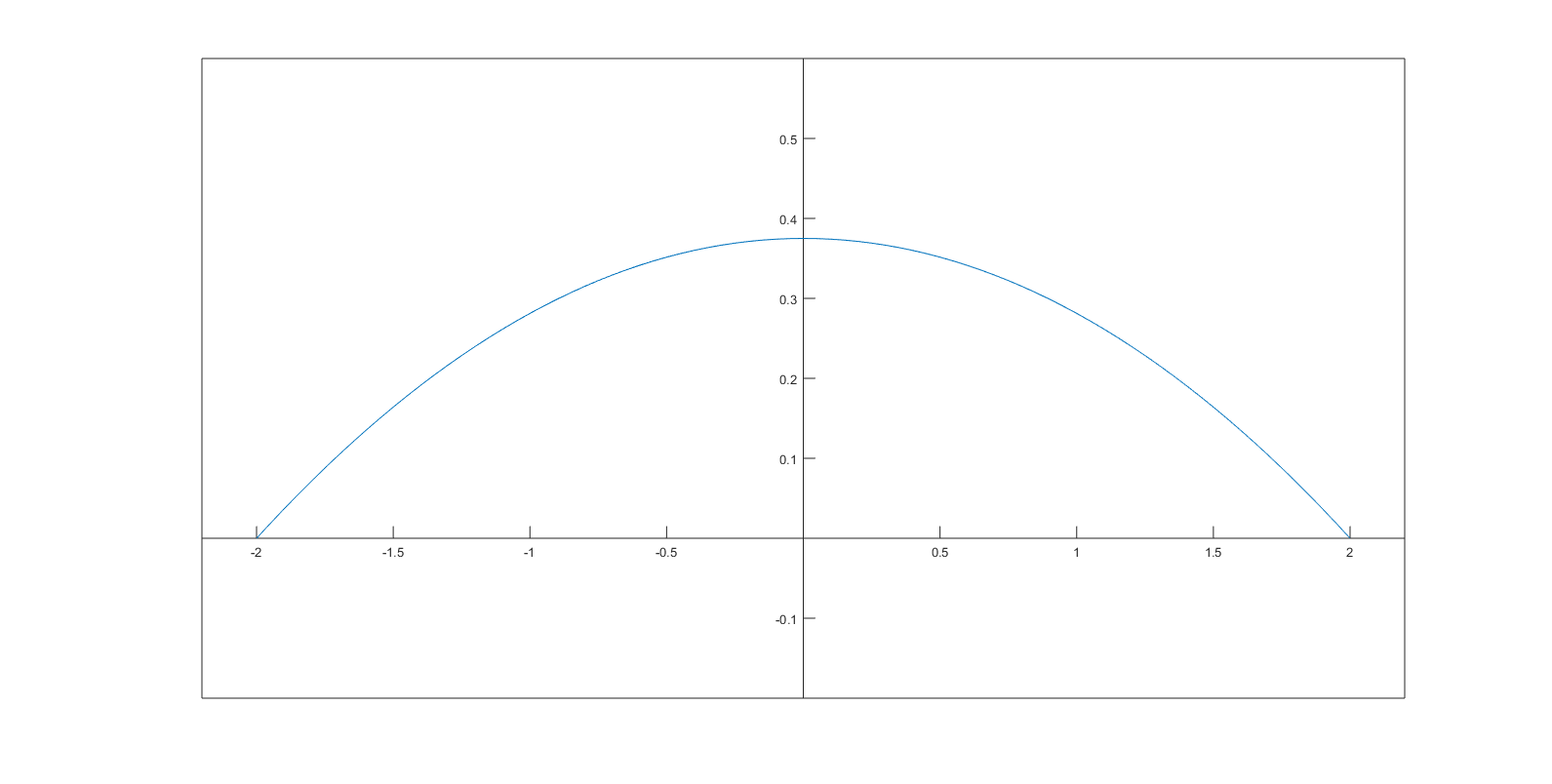
MATLAB:

>> x=-2:0.05:2;
>> y=0.09375*(4-x.^2);
>> plot(x,y)
 

(b)

\[
P(X > 0)=\int_{0}^{2}f(x)dx=\int_{0}^{2}0.09375(4-x^2)dx=0.09375(4x-\frac{x^3}{3})\biggr|_{0}^{2}\approx 0.49999996875
\]

In fact, $P(X > 0)$ should equal to $0.5$, because $f(x)$ is symetric about $y$-axis by the definition of pdf. That is,

\[
P(X > 0)=\int_{0}^{2}f(x)dx=\frac{1}{2}\cdot\int_{-2}^{2}f(x)dx=\frac{1}{2}.
\]

(c)

\[
\begin{split}
P(-1 < X < 1)&=\int_{-1}^{1}f(x)dx=2\int_{0}^{1}f(x)dx\\
&=2\int_{0}^{1}0.09375(4-x^2)dx=2\times 0.09375(4x-\frac{x^3}{3})\biggr|_{0}^{1}\\
&=0.6875000006250
\end{split}
\]

(d)

\[
\begin{split}
P(X < -0.5\ \text{or}\ X > 0.5)&=P(X < -0.5)+P(X > 0.5)=2\cdot P(X > 0.5)\\
&=2\cdot\int_{0.5}^{2}f(x)dx\\
&=2\cdot\int_{\frac{1}{2}}^{2}0.09375(4-x^2)dx\\
&=2\times 0.09375(4x-\frac{x^3}{3})\biggr|_{\frac{1}{2}}^{2}\\
&=0.9999999993750-0.3671874993750\\
&=0.6328125
\end{split}
\]

or

\[
\begin{split}
P(X < -0.5\ \text{or}\ X > 0.5)&=1-P(-0.5\leqslant X\leqslant 0.5)\\
&=1-2\cdot P(0\leqslant X\leqslant 0.5)\\
&=1-2\cdot\int_{0}^{0.5}f(x)dx\\
&=1-2\cdot\int_{0}^{\frac{1}{2}}0.09375(4-x^2)dx\\
&=1-2\times 0.09375(4x-\frac{x^3}{3})\biggr|_{0}^{\frac{1}{2}}\\
&=1- 0.18750(4\times\frac{1}{2}-\frac{1}{8}\cdot\frac{1}{3})\\
&=0.6328125006250
\end{split}
\]