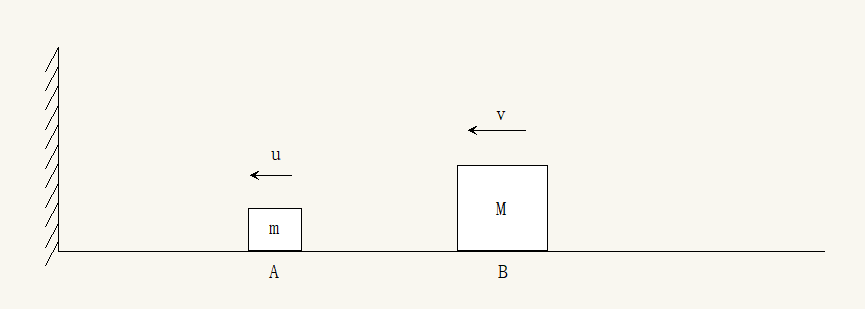
设 $A$, $B$ 在某一次碰撞前的速度分别为 $u_i$, $v_i$; 碰撞后的速度分别为 $u_j$, $v_j$. (当然, 你可以写 $j=i+1$, 这里只起到区别的作用.)
由能量守恒定律(现在是动能守恒), 有
\[
\frac{1}{2}mu_i^2+\frac{1}{2}Mv_i^2=C.
\]
这里 $C$ 是常数. 于是可以改写为
\[
(\sqrt{m}u_i)^2+(\sqrt{M}v_i)^2=r^2.
\]
由于
\[
\frac{\sqrt{M}v_j-\sqrt{M}v_i}{\sqrt{m}u_j-\sqrt{m}u_i}=\frac{\sqrt{M}}{\sqrt{m}}\cdot\frac{v_j-v_i}{u_j-u_i}=\frac{\sqrt{M}}{\sqrt{m}}\cdot(-1)\frac{m}{M}=-\frac{\sqrt{m}}{\sqrt{M}}.
\]
这里第二个等号是因为动量守恒 $mu_i+Mv_i=mu_j+Mv_j$.
令 $u'=\sqrt{m}u$, $v'=\sqrt{M}v$, 则得到下图.
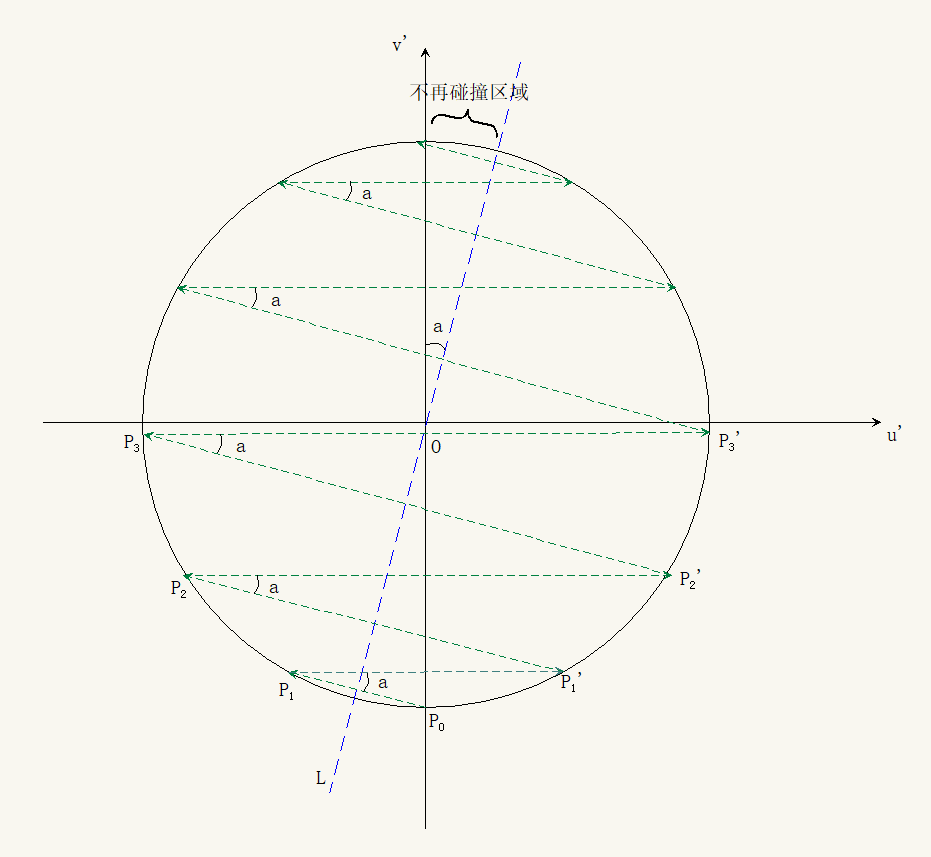
也即, 下一个点 $P_j=(\sqrt{m}u_j,\sqrt{M}v_j)$ 与上一个点 $P_i=(\sqrt{m}u_i,\sqrt{M}v_i)$ 的连线 $\overline{P_i P_j}$ 所在直线的斜率是一个定值, 记为 $k$. 即有
\[k=-\frac{\sqrt{m}}{\sqrt{M}}\]
要使 $A$ 和 $B$ 不再碰撞, 只需 $0 < u_j < v_j$, 即 $\frac{v_j}{u_j} > 1$. 而这等价于
\[
\frac{\sqrt{M}v_j}{\sqrt{m}u_j}>\frac{\sqrt{M}}{\sqrt{m}}=-\frac{1}{k}.
\]
设直线 $L$ 为过原点且与 $\overline{P_i P_j}$ 垂直的直线, $\angle(L, y\text{轴})=\alpha$. 则 $\tan\alpha=\frac{\sqrt{m}}{\sqrt{M}}$.
于是求小方块 $A$ 的碰撞总次数 $N$ 归结为求圆周中共有多少个圆弧 $\labvel{P_i P_j}$. 注意到这些圆弧 $\labvel{P_i P_{i+1}}$, $\labvel{P'_i P'_{i+1}}$ 都是相同的, 因为它们所对的圆周角都是 $\alpha$. 因此,
\[
N=\Bigl[\frac{2\pi}{2\alpha}\Bigr]-1=\Bigl[\frac{\pi}{\alpha}\Bigr]-1.
\]
例如: 当 $m=1$, $M=1$ 时, $\alpha=\frac{\pi}{4}$, $N=\bigl[\frac{\pi}{\pi/4}\bigr]-1=3$.
当 $m=1$, $M=100$ 时, $\tan\alpha=\frac{\sqrt{1}}{\sqrt{100}}=0.1$, $\alpha=\arctan 0.1\approx 0.0996686525$, $N=\bigl[\frac{\pi}{0.0996686525}\bigr]-1=31$.