问题及解答

一只老鼠从洞口爬出后沿一直线运动, 其速度大小与其离开洞口的距离成反比. 当其到达距洞口为 $d_1$ 的 $A$ 点时速度为 $v_1$, 若路径上 $B$ 点离洞口的距离为 $d_2$ ($d_2 > d_1$).

求老鼠由 $A$ 点运动到 $B$ 点所需的时间.

Remark:

题目由 David Chen 提供.

（高等解法）

设距离函数为 $s(t)$, 速度函数为 $v(t)$. 设老鼠从洞口出发的时刻是 $0$, 到达 $A$ 点的时刻是 $t_1$, 到达 $B$ 点的时刻是 $t_2$.

根据题设

\[s(t)v(t)=C\tag{*}\]

这里 $C$ 是常数. 为方便起见, 也简记为 $v\cdot s=C$.

将 (*) 式两边求导, 得

\[
s'(t)v(t)+s(t)v'(t)=0.
\]

注意到 $s'(t)=v(t)$, 代入上式, 得

\[
v^2(t)+s(t)v'(t)=0.
\]

这推出

\[
\frac{dv}{dt}=-\frac{v^2}{s}\quad\Rightarrow\quad-\frac{dv}{v^2}=\frac{dt}{s}\quad\Rightarrow\quad d(\frac{1}{v})=\frac{dt}{s}
\]

因此有

\[
sd(\frac{1}{v})=dt
\]

又 $\dfrac{1}{v}=\dfrac{s}{C}$, 故 $sd(\frac{s}{C})=dt$, 即 $\frac{1}{C}sds=dt$.

\[
\begin{split}
&\frac{1}{C}\cdot\frac{1}{2}ds^2=dt\\
\Rightarrow&\int_{t_1}^{t_2}\frac{1}{C}\cdot\frac{1}{2}ds^2=\int_{t_1}^{t_2}dt\\
\Rightarrow&\frac{1}{2C}\Bigl[s^2(t_2)-s^2(t_1)\Bigr]=t_2-t_1.
\end{split}
\]

因此,

\[
t_2-t_1=\frac{1}{2C}(d_2^2-d_1^2).
\]

又 $C=s(t_1)v(t_1)=d_1\cdot v_1$, 故有

\[
t_2-t_1=\frac{d_2^2-d_1^2}{2v_1 d_1}.
\]

答: 老鼠由 $A$ 点运动到 $B$ 点所花的时间是 $\dfrac{d_2^2-d_1^2}{2v_1 d_1}$.

（初等解法）

假设老鼠在 $B$ 点的速度是 $v_2$.

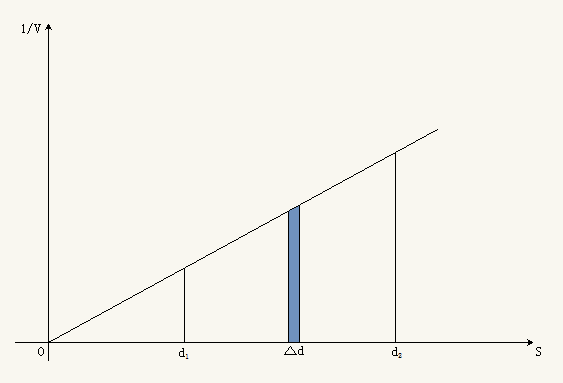
这里 $V(t)$ 是速度函数, $S(t)$ 是距离函数. $t=0$ 对应的是老鼠从洞口出发的时刻.

由题设 $V(t)\cdot S(t)=\text{const.}$, 因此 $1/V$ 和 $S$ 是线性关系, 如图.

当然, 我们也有 $v_1d_1=v_2d_2$, 从而 $v_2=\frac{v_1d_1}{d_2}$.

在物理学中, 我们采用微元法, $\Delta d=\Delta t\cdot V(t)$, 这里 $\Delta d$ 或者记为 $\Delta S$ 是指时刻 $t$ 至时刻 $t+\Delta t$ 所经过的距离. 即 $\Delta t=\frac{1}{V(t)}\cdot\Delta d$.

故图中梯形的面积记为老鼠从 $A$ 点至 $B$ 点所花的时间 $t_2-t_1$,

\[
\begin{split}
t_2-t_1&=\frac{1}{2}(\frac{1}{v_2}+\frac{1}{v_1})\cdot(d_2-d_1)\\
&=\frac{1}{2}(\frac{d_2}{v_1d_1}+\frac{1}{v_1})\cdot(d_2-d_1)\\
&=\frac{d_2^2-d_1^2}{2v_1d_1}.
\end{split}
\]

Remark:

此解答由 David Chen 提供.