问题及解答

将数字 $1,2,3,\ldots,12$ 填入下面的表格, 使得每行、每列以及每个田字格内的四个数字之和都相等.  (Note: 这里的行和列也指包含四个数字的行和列.)

 

 

 

 

 

 

 

 

 

 

 

 

 

Remark:

这是小学四年级的题目. (From 江苏课本练习某难题)

题目来源：张影老师.

 

 

 

 

 

 

 

 

 

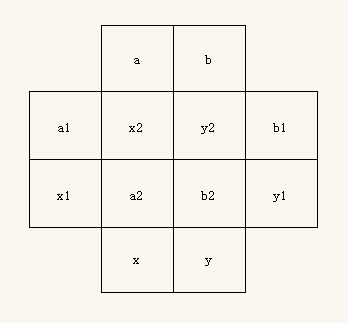
我们首先证明每行、每列以及每个田字格中的四个数字之和均等于 26.

 

如图填入适当的变量符号. 并且设 $a+b=m$, $x+y=n$. 根据要求, 可得

\[
\begin{cases}
a1+b1=a2+b2=m,\\
x1+y1=x2+y2=n,\\
\end{cases}
\]

于是, 我们有

\[
\begin{aligned}
(a+b)+(x+y)=m+n,\\
(a1+b1)+(x2+y2)=m+n,\\
(a2+b2)+(x1+y1)=m+n.\\
\end{aligned}
\]

故,

\[
3(m+n)=\sum_{n=1}^{12}n=\frac{12(12+1)}{2}=78,
\]

推出 $m+n=26$.   Q.E.D.

 

 

当然, 我们还有下面的关系式:

\[
\begin{cases}
a1+x1=b2+y2,\\
a2+x2=b1+y1,\\
a+x=a1+x1,\\
b+y=b1+y1.\\
\end{cases}
\]

 

---

 

经过编程计算,  在不排除同构(或等价)的意义下, 共计有 912 个解.

这里举几个例子:

 

	1	6
2	12	7	5
8	4	3	11
	9	10

 

将其顺时针旋转 $90^{\circ}$, 得到与之等价的解:

 

	8	2
9	4	12	1
10	3	7	6
	11	5

 

因此有 $912/4=228$ 个解.