问题及解答

Langley 问题是一道比较有名的初等几何题目, 有很多证明方法或求解方法. (https://www.cut-the-knot.org/triangle/80-80-20/IndexToClassical.shtml 上给出了12种方法.)

其中最巧妙也是最简洁的,  是由下面PDF文件给出的证明. 只需添加两条辅助线即可完成证明.

http://www.arbelos.co.uk/Papers/Triangle-problem.pdf

 

---

问题：

在三角形 $ABC$ 中, $\angle A=20^{\circ}$, $AB=AC$. 点 $D$ 位于边 $AC$ 上使得 $\angle DBC=60^{\circ}$ 并且点 $E$ 位于边 $AB$ 上, 使得 $\angle ECB=50^{\circ}$.

求 $\angle BDE$ 的大小.

 

 

这里给出上面pdf文件中的截图

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Remark:

类似的证明方法, 都会在其中找到一个正三角形.

 

References:

https://www.cut-the-knot.org/triangle/80-80-20/index.shtml

 

这里的证法是 Minghai LIU 给出的.

 

 

修正: 图中 (4) 应该修改为

\[
FD\parallel BC\Longrightarrow\triangle FDG\ \text{是等边三角形}\ \Longrightarrow FD=DG.
\]
 

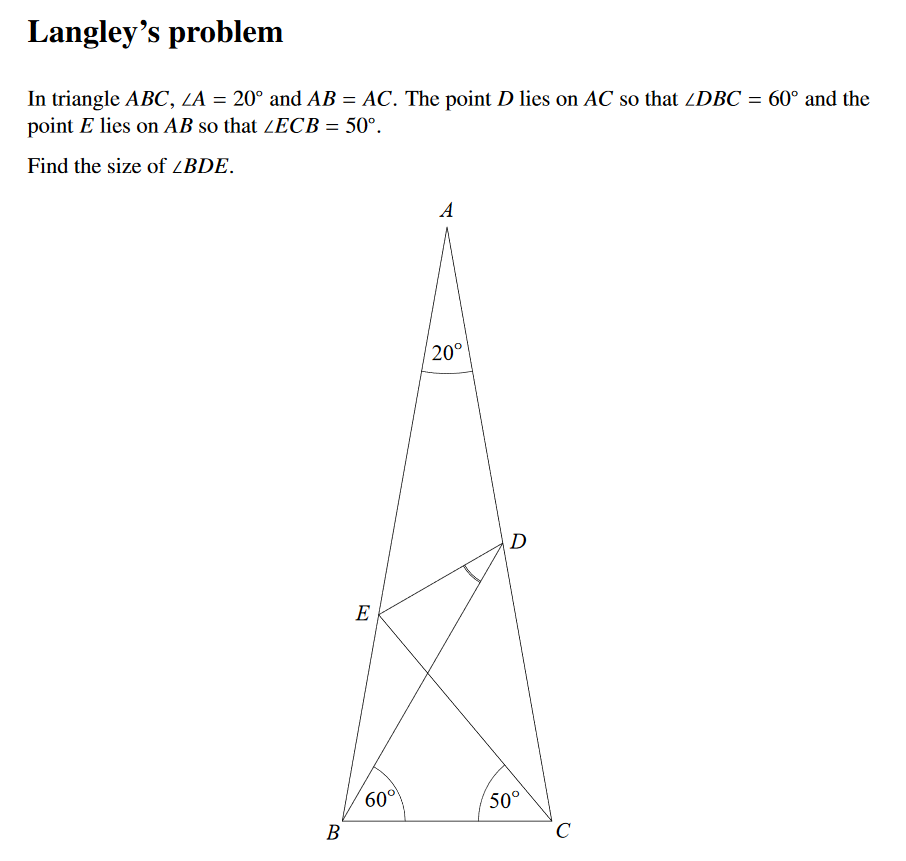
我们给出一个不添加辅助线的证明方法（或求解方法）.

 

 

 

 

 

 

 

 

 

 

 

 

记 $\theta=\angle BDE$. 不妨设 $BC=1$. 于是 $BE=BC=1$.

在 $\triangle BDE$ 中, 由正弦定理, 得

\[
\frac{DE}{\sin 20^{\circ}}=\frac{BE}{\sin\theta}=\frac{1}{\sin\theta}\Longrightarrow DE=\frac{\sin 20^{\circ}}{\sin\theta}.
\]

由于 $\triangle BCE$ 是等腰三角形. 故 $EC=2\cdot BE\sin 40^{\circ}=2\sin 40^{\circ}$.

在 $\triangle CDE$ 中, 根据正弦定理, 有

\[
\frac{EC}{\sin(\theta+40^{\circ})}=\frac{DE}{\sin 30^{\circ}}.
\]

将 $EC$ 和 $DE$ 代入上式, 得

 

 

 

\[
\begin{split}
&\frac{2\sin 40^{\circ}}{\sin(\theta+40^{\circ})}=\frac{\frac{\sin 20^{\circ}}{\sin\theta}}{\frac{1}{2}}\\
\Longrightarrow\ &\frac{2\cos 20^{\circ}}{\sin(\theta+40^{\circ})}=\frac{1}{\sin\theta}\\
\Longrightarrow\ &\sin(\theta+40^{\circ})=2\sin\theta\cdot\cos 20^{\circ}\\
\Longrightarrow\ &\sin(\theta+40^{\circ})=2\sin\theta\sin 70^{\circ}\\
\Longrightarrow\ &\sin\theta\cos 40^{\circ}+\cos\theta\sin 40^{\circ}=2\sin\theta\sin(30^{\circ}+40^{\circ})\\
\Longrightarrow\ &\sin\theta\cos 40^{\circ}+\cos\theta\sin 40^{\circ}=2\sin\theta\cdot(\sin 30^{\circ}\cos 40^{\circ}+\cos 30^{\circ}\sin 40^{\circ})\\
\Longrightarrow\ &\sin\theta\cos 40^{\circ}+\cos\theta\sin 40^{\circ}=\sin\theta\cos 40^{\circ}+\sqrt{3}\sin\theta\sin 40^{\circ}\\
\Longrightarrow\ &\cos\theta\sin 40^{\circ}=\sqrt{3}\sin\theta\sin 40^{\circ}\\
\Longrightarrow\ &\cos\theta=\sqrt{3}\sin\theta\\
\Longrightarrow\ &\tan\theta=\frac{\sqrt{3}}{3},
\end{split}
\]

因此 $\theta=30^{\circ}$.   证毕.

 

---

Remark:

 

这个证明与 https://www.cut-the-knot.org/triangle/80-80-20/Classical3.shtml#solution 上给出的是一样的.