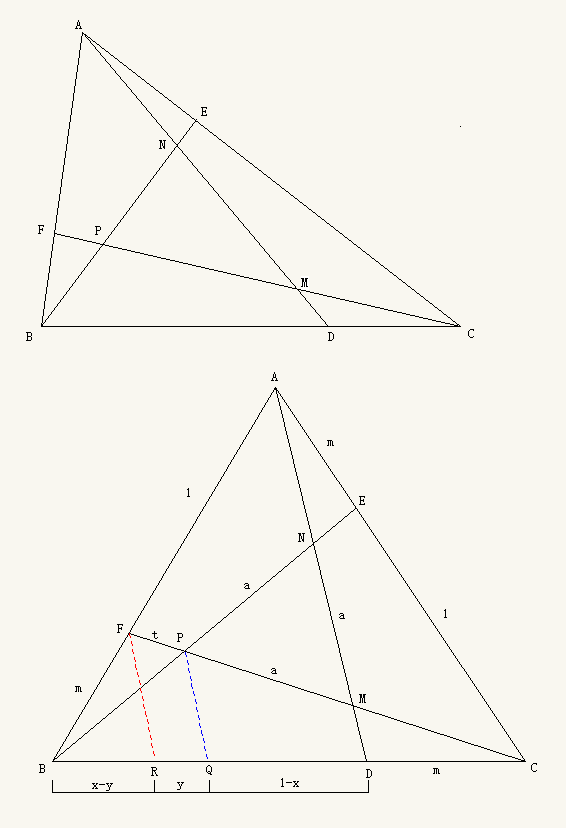
在三角形 $\triangle ABC$ 中, $D,E,F$ 分别是三边 $BC$, $CA$, $AB$ 上的点, 且满足 $\frac{AF}{FB}=\frac{BD}{DC}=\frac{CE}{EA}=\frac{1}{m}$. 设 $AD$ 与 $BE$ 交于 $N$ (有时可记为 $AD\cap BE=N$), $BE\cap CF=P$, $CF\cap AD=M$. 求两三角形面积之比 $S_{\triangle MNP} : S_{\triangle ABC}$.
在三角形 $\triangle ABC$ 中, $D,E,F$ 分别是三边 $BC$, $CA$, $AB$ 上的点, 且满足
\[
\frac{AF}{FB}=\frac{BD}{DC}=\frac{CE}{EA}=\frac{1}{m}.
\]
设 $AD$ 与 $BE$ 交于 $N$ (有时可记为 $AD\cap BE=N$), $BE\cap CF=P$, $CF\cap AD=M$. 求两三角形面积之比 $S_{\triangle MNP} : S_{\triangle ABC}$.
[Hint] 使用仿射几何的性质.
References:
冯克勤 射影几何漫谈