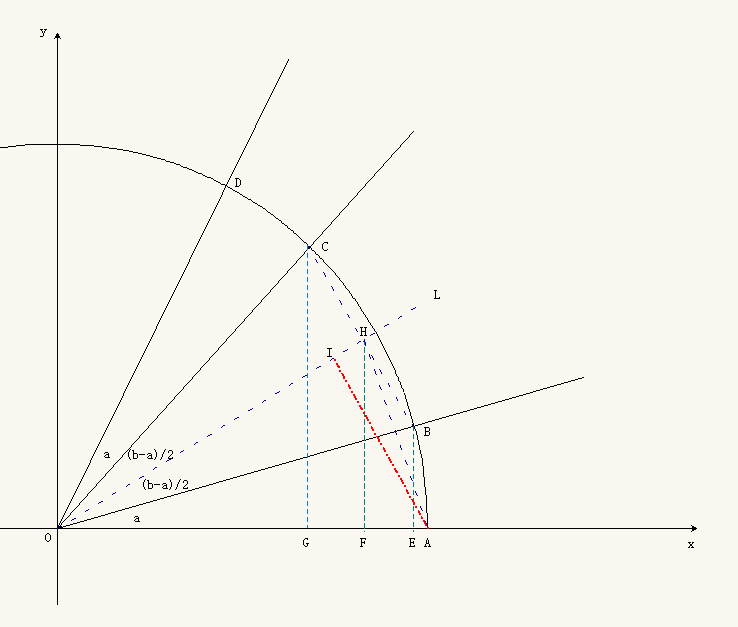
三角函数和差化积公式的推导
\[
\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\tag{1}
\]
\[
\sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}\tag{2}
\]
\[
\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\tag{3}
\]
\[
\cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}\tag{4}
\]
和差化积公式可以转换为积化和差公式. 例如, 由 (3) 可推出
\[
\cos\alpha\cdot\cos\beta=\frac{1}{2}\bigl(\cos(\alpha+\beta)+\cos(\alpha-\beta)\bigr).
\]
Remark:
我们只需要证明 (1), 因为其余的可以由 (1) 推出.
我们这里给出的关于 (1) 的参考证明利用了几何方法. (这个几何图形是一个很熟悉的直角梯形. 类似的直角梯形在问题2021中也出现过.)
Remark:
如果 (3)-(4), 则得
\[
\cos\beta=\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}+\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
\]
此时, 若令 $x=\dfrac{\alpha+\beta}{2}$, $y=\dfrac{\alpha-\beta}{2}$, 则 $x-y=\beta$, 于是得到
\[
\cos(x-y)=\cos x\cos y+\sin x\sin y.
\]