直角三角形中由两条平行于某一直角边的直线(这三条直线的间隔相等)构成了两个梯形, 它们的面积决定了另一个三角形的面积.
直角三角形 $\triangle ABC$ 中 $\angle B$ 是直角, DE, FH 均平行于 AB, (D、F在线段 AC 上, 且 $D\neq A,C$. E、H 在线段 BC 上)。 H 是线段 BE 的中点.
假设梯形 ABHF 的面积为 $S_1$, 梯形 FHED 的面积为 $S_2$, 求三角形 DEC 的面积 $S_3$.
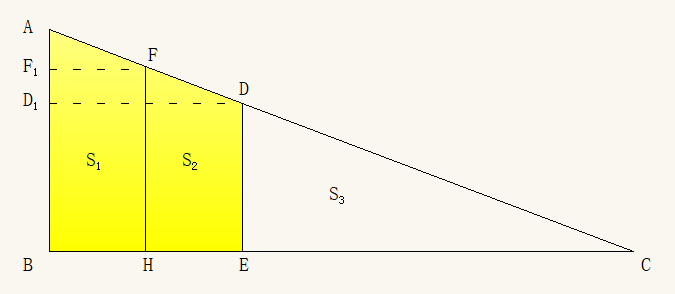
直角三角形 $\triangle ABC$ 中 $\angle B$ 是直角, DE, FH 均平行于 AB, (D、F在线段 AC 上, 且 $D\neq A,C$. E、H 在线段 BC 上)。 H 是线段 BE 的中点.
假设梯形 ABHF 的面积为 $S_1$, 梯形 FHED 的面积为 $S_2$, 求三角形 DEC 的面积 $S_3$.

1
过点 $F$ 和 $D$ 分别做平行于 BC 的直线, 交线段 AB 分别于 $F_1$, $D_1$.
设 $BH=HE=d$, $AF_1=F_1 D_1=\delta$. $HC=x$, $FH=y$.
于是
\[
\frac{S_1}{S_2}=\dfrac{\frac{1}{2}(y+y+\delta)d}{\frac{1}{2}(y+y-\delta)d}=\frac{2y+\delta}{2y-\delta},
\]
这推出
\[
\frac{\delta}{y}=\frac{2(S_1-S_2)}{S_1+S_2}.
\]
类似的, 可得
\[
\frac{d}{x}=\frac{\delta}{y}=\frac{2(S_1-S_2)}{S_1+S_2}.
\]
注意到 $S_3=\frac{1}{2}(x-d)(y-\delta)$, 两边同除以 $xy$, 注意到 $xy=2(S_2+S_3)$. 得
\[
\frac{S_3}{xy}=\frac{1}{2}\cdot\frac{x-d}{x}\cdot\frac{y-\delta}{y}.
\]
\[
\begin{split}
\Rightarrow\ &\frac{S_3}{S_2+S_3}=(1-\frac{d}{x})(1-\frac{\delta}{y})\\
\Rightarrow\ &\frac{S_2+S_3}{S_3}=\frac{1}{(1-\frac{d}{x})^2}\\
\Rightarrow\ &1+\frac{S_2}{S_3}=\dfrac{1}{(1-\frac{2(S_1-S_2)}{S_1+S_2})^2}=\frac{(S_1+S_2)^2}{(3S_2-S_1)^2}\\
\Rightarrow\ &\frac{S_2}{S_3}=\frac{(S_1+S_2)^2}{(3S_2-S_1)^2}-1=\frac{8S_2(S_1-S_2)}{(3S_2-S_1)^2}\\
\Rightarrow\ &S_3=\frac{(3S_2-S_1)^2}{8(S_1-S_2)}.
\end{split}
\]