
Galileo Galilei (1564-1642),意大利物理学家、数学家、天文学家及哲学家,科学革命中的重要人物。其成就包括改进望远镜和其所带来的天文观测,以及支持哥白尼的日心说。Galileo 被誉为“现代观测天文学之父”、“现代物理学之父”、“科学之父”及“现代科学之父”。
Stephen William Hawking 说,“自然科学的诞生要归功于 Galileo,他这方面的功劳大概无人能及。”
Einstein 称他为现代科学之父。


Galileo Galilei (1564-1642),意大利物理学家、数学家、天文学家及哲学家,科学革命中的重要人物。其成就包括改进望远镜和其所带来的天文观测,以及支持哥白尼的日心说。Galileo 被誉为“现代观测天文学之父”、“现代物理学之父”、“科学之父”及“现代科学之父”。
Stephen William Hawking 说,“自然科学的诞生要归功于 Galileo,他这方面的功劳大概无人能及。”
Einstein 称他为现代科学之父。

他是第一个提出关于自然界的严肃问题的人;也是科学历史上第一个做物理实验的人。
通过让物体沿倾斜且磨光的表面滑下,同时用他的脉搏测量时间,他发现了力学的基本定律。
他很钦佩 Euclid 和 Archimedes, 非常重视数学在应用科学方法上的重要性,在 Pisa 大学和 Padua 大学任教时给学生开设了数学课。他了解关于圆锥曲线的 Appolonius 理论,利用实验和数学他设法去描述抛物体的运动轨迹。

关于物体运动完整的理论是 Newton 建立起来的。他将经典力学(特别地,由 Galileo 发现)的定律翻译成了计算的语言。
Newton(1643-1727)是人类历史上最伟大的天才。他在1687年的著作《自然哲学之数学原理》提出了“万有引力定律”,并对三大运动定律作了描述,为现代自然科学奠定了基础,并且创立了宇宙的体系。
Newton 还和 Leibniz 各自独立地发明了微积分。
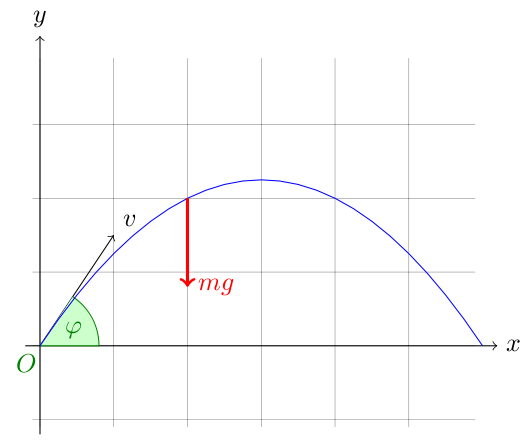
一个质量为 m 的物体,仅被外力(重力) F=-mg 竖直向下作用在上面。根据 Newton 的力学定律。以初速 v,初始仰角 φ ,从原点抛出的物体在平面 oxy 内的轨迹 (x(t),y(t),z(t)) 应满足方程
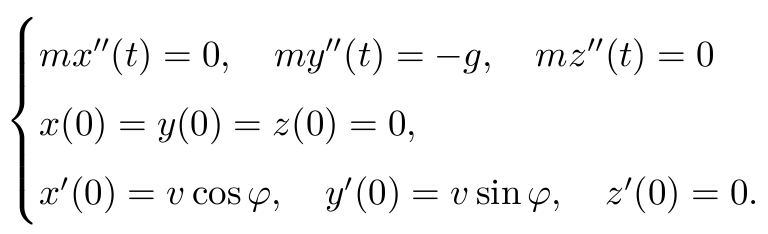

对这些方程积分, 得到
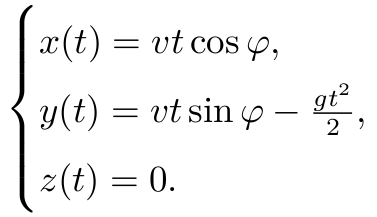
从而抛物体的轨迹为
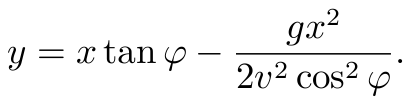

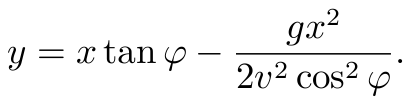
这是一个抛物线方程, 抛物线是最重要的图形之一, 自然界的定律就是用这些几何图形所组成的语言写成的.

作为 Tycho Brache 的接班人,Kepler 认真地研究了 Tycho 多年对行星进行仔细观察所做的大量记录。
在进行了多年艰苦的研究之后,Kepler 第一个得出了在某种程度上出乎意料的结论:太阳系的行星是沿着圆运动的。
圆是引人注目的,因为圆是古代数学中的一个基本几何对象,并且人们都相信任何合理的事物都作圆运动,或是圆运动的复合。
但,糟糕的是:太阳本身并不位于圆的中心!

这在 Kepler 看来似乎非常奇怪。于是他开始重新计算每个数据,甚至比之前更加仔细了。
后来,他发现,事实上,这些行星都是沿着椭圆运动的,但离心率都很小(这也是他一开始误认为圆的原因)。太阳位于其中一个焦点上。
这个断言就是现在众所周知的 Kepler 第一定律。
Kepler 于1609年发表了第一定律与第二定律(面积定律)。
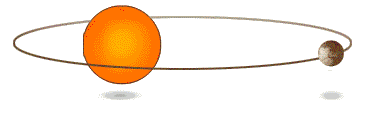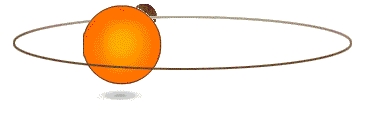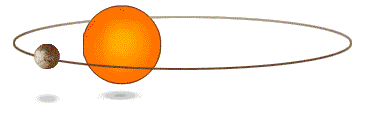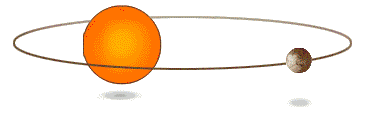
Kepler 第一定律,也称椭圆定律:每一个行星都沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点中。
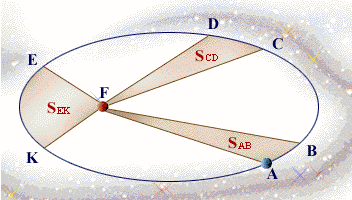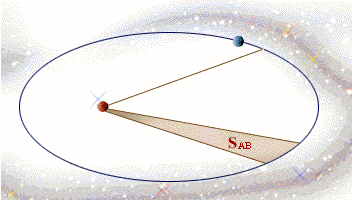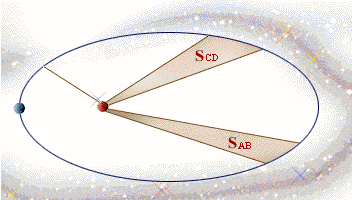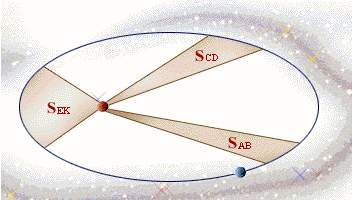
Kepler 第二定律,也称面积定律:在相等时间内,太阳和运动着的行星的连线所扫过的面积都是相等的。
这一定律实际揭示了行星绕太阳公转的角动量守恒。用公式表示为
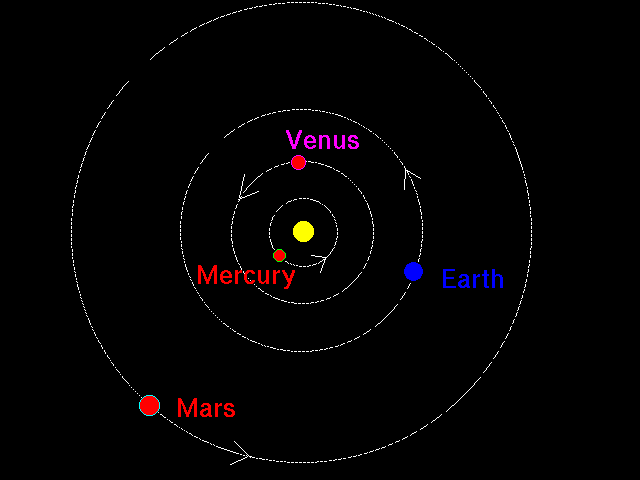
Kepler 第三定律, 也称调和定律或和谐定律: 各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比.
若 a 是椭圆轨道的半长轴, τ 是行星公转周期, 则
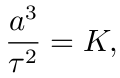
其中 K 是一常数, 仅与所围绕的天体有关, 与行星无任何关系. 简言之, 围绕同一天体运行的行星所计算出来的 K 相等.
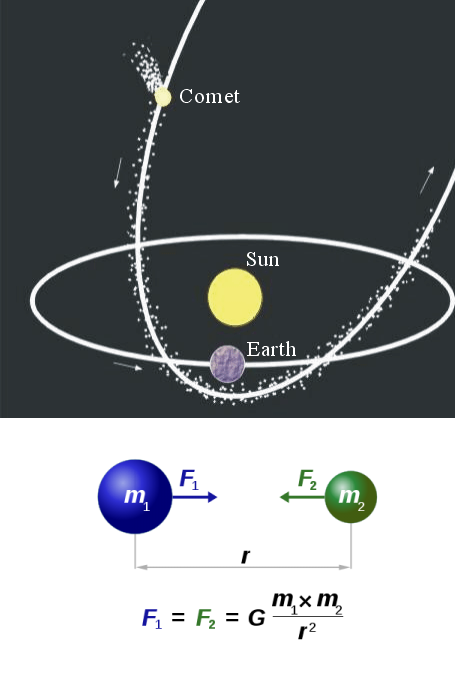
我们从 Newton 第二运动定律和万有引力定律开始。
这里我们考虑质量为 m 的行星或彗星绕太阳作运动, 并忽略宇宙中其他天体对其的影响。
根据万有引力定律,太阳作用在行星或彗星上的力等于
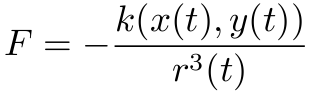
其中 ![]()

应用 Newton 第二定律 F=ma, 我们有
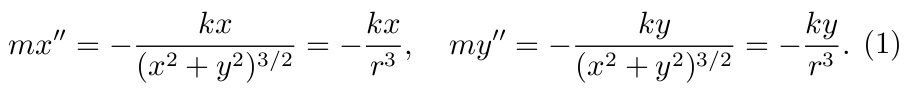
在极坐标 x=rcosφ, y=rsinφ 之下,我们有
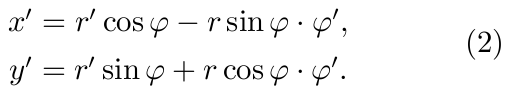

于是有

由(3)和(1),我们有 x''sinφ-y''cosφ=0 (4), 事实上
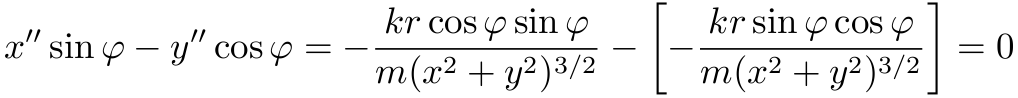

由(1)-(4), 通过微分, 可得出两个著名的守恒定律

(5)表述了能量守恒律,(6)就是我们之前提到的 Kepler 面积定律.

事实上
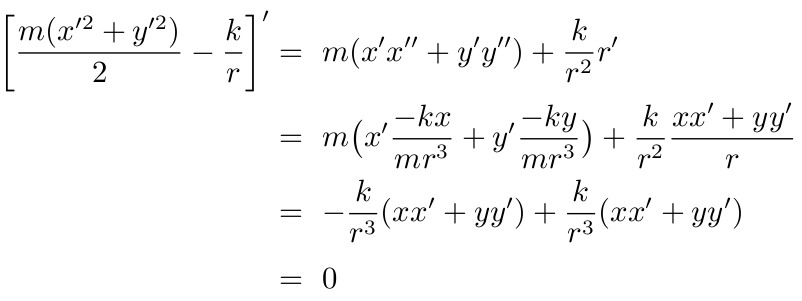
因此(5)成立.

由(3)(a)
进行微分, 得
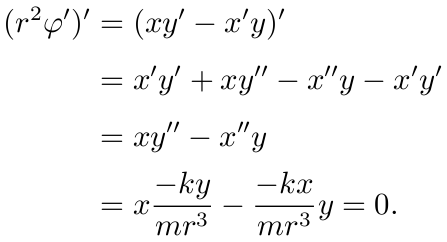

故(6)式是成立的.
实际上该式说的就是单位时间内的面积增量是恒定的. Kepler 第二定律得证. 下面我们来推导行星或彗星的运动轨迹.
(5), (6), (3)(b) 可推出等式

证明: 由(6), 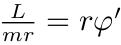

因此
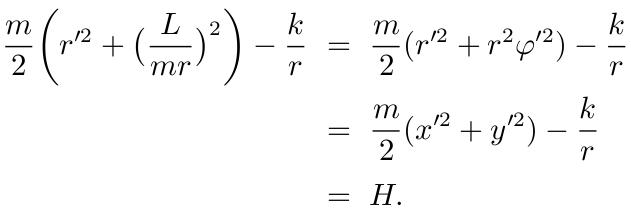
由此式得到下面的微分方程
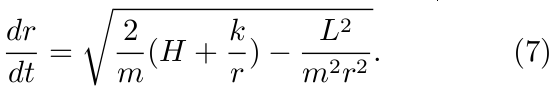

(这里不妨假设 r'>= 0.) 根据 Kepler 面积定律(6), 我们有
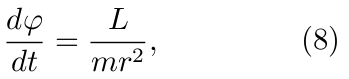
由(7)和(8)可导出下面的微分方程
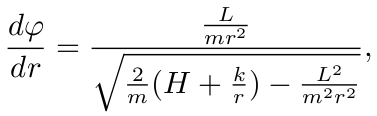
这个方程是可积的, 积分此方程, 得

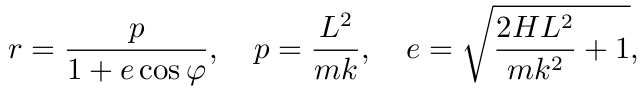
因此, 当 H<0 时轨道是椭圆的, H=0 时轨道是抛物的, H>0 时则是双曲的.
证明:

令
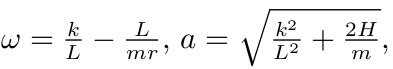
则
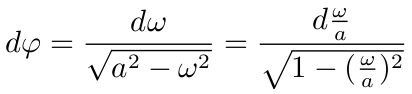
积分得
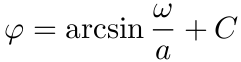
其中 C 是常数. 从而 ![]() .
.
![]()
即
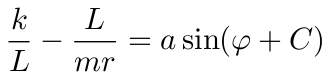
解得
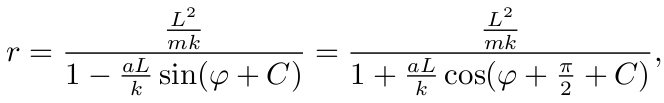
将上式写成 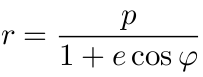 的形式, 则其中
的形式, 则其中
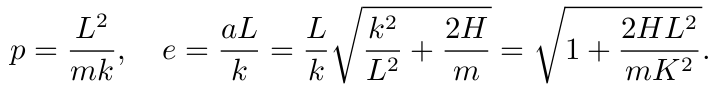
Q.E.D

H.Minkowski(1864--1909), 著名的德国数学家和物理学家, 是希尔伯特的好朋友. 1886年, 他建立了凸集理论的基础(见《数的几何》(Geometry of Numbers).他将几何化思想实现于物理, 也就是, 通过引进具有双曲度量的4维空间, 给出了狭义相对论的一个几何解释(我们马上讲这个问题).他曾在 Königsberg 大学、Berlin 大学、Zurich 大学和 Göttingen 大学任教. Einstein 是他在 Zurich 大学的一个学生. Einstein 并没有给 Minkowshi 留下深刻映象, 他发现 Einstein 智力太迟钝.
记住下面一句话是很有帮助的, 不是所有注定要为科学作贡献的人都在讨论班和科学奥林匹克大会上表现敏捷的.

美籍德国犹太裔, 理论物理学家, 相对论的创立者, 现代物理学奠基人. 1921年获诺贝尔物理学奖, 1999年被美国《时代周刊》评选为“世纪伟人”.
The world is simple. Very simple. But no more than that!
--- Albert Einstein
让我们在一个相对比较简单的例子中尽量理解关于狭义相对论的基本公式.
想象一下下面的场景.
一列火车沿着一条直线型的铁轨上以速度 v 匀速行驶. 在第三个车厢的平台上, 站着一位吸烟者 S. 在吸烟者 S 向站台上一个助理车站管理员 M 射击的那一刻, 车厢里有一个乘客 P 在以相对车厢速度 v' 匀速走动. 假设吸烟者 S, 车站管理员 M 以及那位乘客 P 都有精密的计时器.
我们来确定一下乘客 P 关于助理车站管理员 M 的速度.
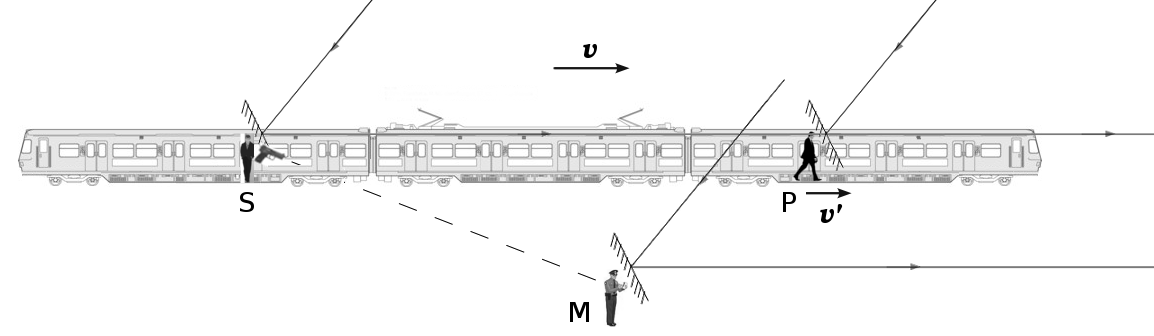
S: 吸烟者; P: 乘客; M: 车站管理员
等一下, 任何一位神志清醒, 心智健全的人都会马上回答说:
这么很简单, 不就是 V=v+v'吗?
干吗还要一个吸烟者 S, 跟他有什么关系? 而且还非得要开枪? 为什么每个人还要带计时器?而且还得是精密的.
Newton 笑了笑, 回答道: 我认为也是这样的.
Einstein 思考了一下(当然不是一会会, 要么他早已经熟悉了:)), 说道: 好像不是这么简单的相加吧, 我认为是
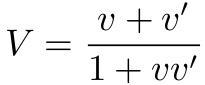
在 Einstein 看来, 速度空间中两个速度的和应该是这样相加的.
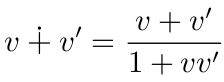
于是我们看到了下面具有讽刺意味的场景:
自然和自然定律隐藏在深夜里.
上帝说: "Let Newton be!" 于是世间充满了光线.
但是撒旦将 Einstein 带到了前面.
现在所有都是黑暗, 跟以前一样.
这首诗的前两行是英国诗人 Alexandre Pope (1688-1744) 写的.
在有了足够多的几何知识后, 让我们来尽力去理解一下相对论理论的情形是否如这首诗的作者所描绘的那样黑暗.
首先, 我们应当提一下, Newton 没有意识到一个重要事实(它在20世纪初才由实验建立起来). 这个事实是:
光在任何一个惯性坐标系中都具有恒定的速率.
即光速不变性.
而且没有其他东西运动的速率可以超过光.
于是, 如果在初始时刻, 所有三个人
都可以使用镜子将阳光反射沿着铁轨方向运动, 则这些光线将互不落后也不比任何其他光线快.
这将导致 M, S, P 三个人的精密计时器的运作有差异! 并且, 不可以将空间与时间割裂开来进行独立地思考.
我们有三个等价的坐标系: 分别相对于 M, S, P.
它们等价是因为它们都是惯性系.
在时刻的每一瞬, M, S, P 的三个精密计时器都有读数 t,t',t''.
并且每个精密计时器在各自的坐标系中有自己的坐标(空间坐标和时间坐标).
记住时间和空间不可以割裂来考虑.(如果还是有疑问的话, 就暂时承认这一点, 或者不妨认为常识中时间和空间“独立”是特殊情形.)
假设在某一时刻,
我们假设惯性系的 Galileo 定律 是有效的, 据此, 所有惯性系是等价的. (形象地说, 如果 S 所在车厢中窗户的窗帘都拉上, 并且没有其他提示, 如火车运动的声音或显示屏等, 则他不能判断火车是否在运动.)
于是, 自然地可以假设 (x,t) 与 (x',t') 之间的关系是线性的. 这是相对论理论最重要的假设.
(如果坐标变换是非线性的, 则事情会变得相当含糊.)
最后为方便起见, 我们对时间做尺度变换以使得光速等于 1.(就像播放录像时快进或慢进一样, 好像时间作了伸缩变换.)
现在所有假设已经建立了, 我们可以开始推导 Einstein 的结论了.
假设 S 在时间的初始时刻反射一太阳光线, 并且此光线被 M 测到是在时刻 t,
在 M 的坐标系中 光线运动了距离 x.
在火车坐标系(或 S 坐标系)下, 光线运动了 x', 在时刻 t' 被测到到达了 M.
这也就是为什么一开始要有吸烟者这个人, 并且还假设了他朝 M 无故开枪这个场景.
事实上, 你会发现,
M 站在站台上哪个位置并不重要.
比如就假设 M 是放在轨道某处的一个安装有精密计时器的靶子就行了, 这样这些对象就在同一条直线上了.
根据光速不变猜测, 有
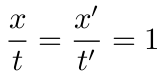
即, 关于坐标系的线性变换必须保持 x2-t2 的形式. (注意位移可能是负的, 所以可能是 -x=t).
这样的变换我们很熟悉, 就是双曲变换(双曲变换与旋转变换类似, 而且并不比它复杂到哪.)
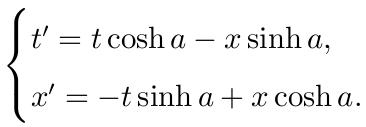
不妨验证一下, 在此变换下
证明:
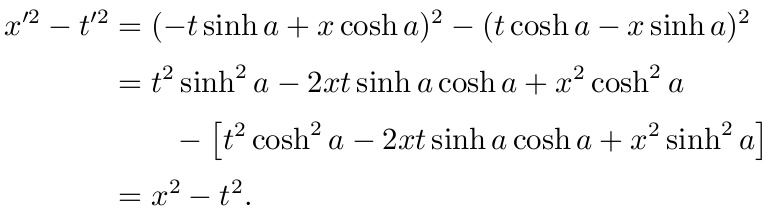
Q.E.D
后面讲 Lorentz 变换时会详细介绍如何得到这个变换的.
现在考虑 M 的精密计时器读到 t 的那一时刻,
令此时刻吸烟者 S 在自己坐标系(或火车坐标系)中的坐标为 (0,t').
(吸烟者一直在抽烟, 没有走来走去, 因此空间坐标一直是 0, 而精密计时器的读数已经到达 t'.)
由于 x'=0, 从(4)的第二式推出
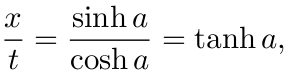
这里 x 是 M 坐标系中 S 的空间坐标, 因此 x/t 可以认为是火车速度, 从而
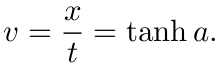
现在距离导出 Einstein 公式只有最后几步了. 仅是数学运算而已.
在 M 坐标系中, 乘客 P 的坐标是 (Vt,t),
在 S 坐标系(或火车坐标系)中坐标为 (v't',t').
这样根据变换(4), 得到
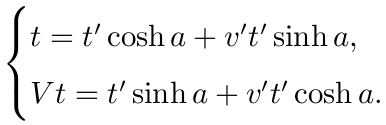
证明:此时 x=Vt, x'=v't', 由(4), 得
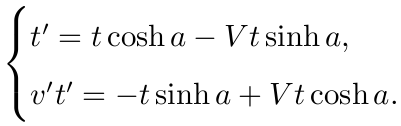
即
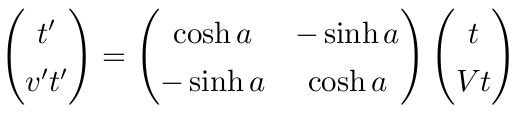
从而
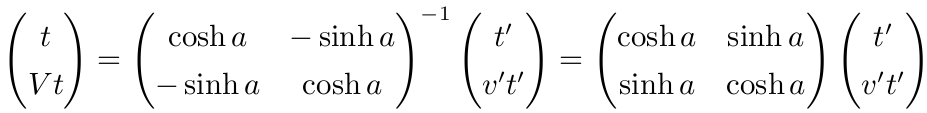
故
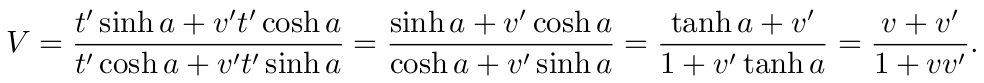
Einstein 的断言被证明了是正确的, 当然是要在这些假设的前提之下.
事情并没有诗人想象地那么糟糕. 用 Einstein 的话来讲, 所有事情相当简单, 甚至是非常简单.
让我们问个问题, 既然如此简单, 是否可用一句话来表达狭义相对论的本质?
对于几何学硕士生或者学过非欧几何的学生来讲应该是不难理解的.
考虑 [-1,1] 上的映射
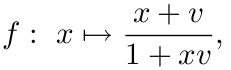
其中 v 是绝对值小于 1 的固定值. 这不就是 Einstein 的那个速度加法公式吗? 正是. 这个映射有什么性质呢?
容易验证f是 [-1,1] 映到自身的一一在上映射.
证明: 假设f(x1)=f(x2), 则
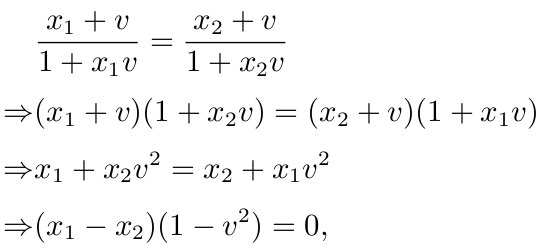
由于 |v|<1, 这里 1 是光速. 故 x1=x2, 所以 f 是单射. 并且容易验证 f'(x)>0.
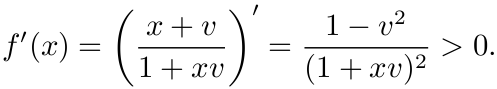
此外,

由于 |v|<1, 故推出 x2-1<= 0, 即 |x|<=1.
一般物体的速度达不到光速, 所以 |x|<1, 因此只需考虑映射
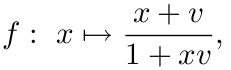
其中
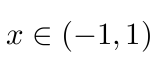
这就是一维 Lobachevsky 直线模型. 这个模型在另一方面就是刚才狭义相对论中的速度之和公式.
如果所考虑的运动是二维的, 则狭义相对论的速度之和公式对应到二维 Lobachevsky 平面模型, 三维空间的运动则对应到 Lobachevsky 三维模型.

Nikolai Ivanovich Lobachevsky (Russian: Никола́й Ива́нович Лобаче́вский) (1792—1856), 俄罗斯最伟大的科学家之一, 也是非欧几何的早期发现人之一. 他被英国著名的数学家 William Clifford 称为几何学界的 Copernicus.
Lobachevsky 在尝试证明平行公理时发现以前所有的证明都无法逃脱循环论证的错误. 于是, 他作出假定: 过直线外一点, 可以作无数条直线与已知直线平行. 如果这假定被否定, 则就证明了平行公理. 然而, 他不仅没有能否定这个命题, 而且用它同其他欧氏几何中与平行公理无关的命题一起展开推论, 得到了一个逻辑合理的新的几何体系——非欧几里得几何学, 这就是后来人们所说的 Lobachevsky 几何.

Lobachevsky 几何的创立对几何学和整个数学的发展起了巨大的作用, 但一开始并没有引起重视, 直到他去世后12年才逐渐被广泛认同. Lobachevsky 在数学分析和代数学方面也有一定成就.
非欧几何是人类认识史上一个富有创造性的伟大成果, 它的创立, 不仅带来了近百年来数学的巨大进步, 而且对现代物理学、天文学以及人类时空观念的变革都产生了深远的影响.
不过, 这一重要的数学发现在 Lobachevsky 提出后相当长的一段时间内, 不但没能赢得社会的承认和赞美, 反而遭到种种歪曲、非难和攻击, 使非欧几何这一新理论迟迟得不到学术界的公认.
我们现在可以用一句话来给狭义相对论作解释了:
狭义相对论中的速度空间不是其它, 正是 Lobachevsky 模型;
对于所考虑运动的维数(1维,2维,3维), 分别对应到 Lobachevsky 直线, Lobachevsky 平面, Lobachevsky 空间.
这就是物理与几何的联系, 几何成了描述物理学的强有力的语言.

Hendrik Antoon Lorentz,1853~1928,荷兰物理学家、数学家,
由于发现并从理论上解释了 Zeeman 效应, 1902年 Lorentz 与 Pieter Zeeman 一起获得 Nobel 物理学奖. Einstein 用来描述空间和时间的变换方程就是他发现的, 即 Lorentz 变换.
下面我们就从数学的角度来推导 Lorentz 变换.
Lorentz 变换在狭义相对论中扮演的角色与 Galileo 变换在经典力学中所扮演的角色是一样的.
首先复习一下 Galileo 变换
Galileo 变换是指
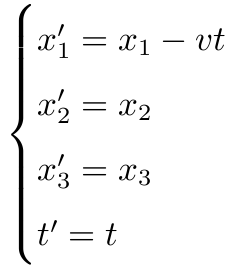
经典力学中的定律在 Galileo 变换之下不变.
广义 Galileo 变换形如
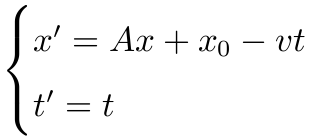
其中 A 是正交矩阵, v 是速度向量
即 (x') 参照系相对于固定参照系 (x) 以恒定速度 v 作运动.
Galileo 变换保持欧氏度量
且保持时间间隔不变(即对于时间来说是等距变换).
所有这些变换构成一个群, 称为 Galileo 群.
下面我们回忆一下 Minkowshi 空间 R41,3 的定义.
作为向量空间, R41,3 与 R4 没有分别.
只不过这里对于向量 ξ=(x0,x1,x2,x3), 定义下面的范数
显然, 这里 |ξ|2 可正可负.
具体看下面 R31,2 的图.
注: 粒子的世界线(world line)一定位于光锥或光锥内部, 因为其速度小于等于光速. 所谓世界线就是粒子在 Minkowshi 空间中运动的轨迹.
我们要考察的 Lorentz 变换就是指 Minkowshi 空间 R41,3 到其自身的保持上述范数的映射.
为了与狭义相对论相结合, 一般令 x0=ct,
其中 c 是光速, t 是时间, x1,x2,x3 是空间坐标.
Lorentz 变换即是保持下面 Minkowshi 度量的映射.
一般还要求 Lorentz 变换保持原点不动, 不过这并不重要.
下面我们所讲的 Lorentz 变换都是指保持原点不动的.
Minkowski 空间的所有 Lorentz 变换 组成一个群, 称为 Poincaré 群.
前面我们看到类时向量的范数大于 0,
所以对于类时(可微)曲线(即切向量均位于光锥内部的曲线),
可仿照欧氏空间定义其长度.
对于类时曲线 γ(t)
定义其长度
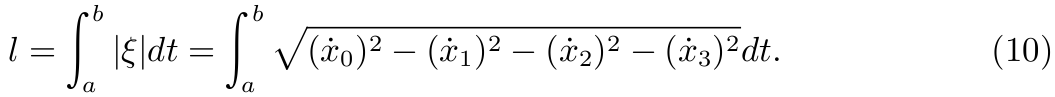
狭义相对论中, 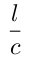 称为 proper time.
称为 proper time.
下面解释为什么称为 proper time.
若一个粒子在 3 维欧氏空间中作匀速运动, v=(v1,v2,v3), 即
则, 由(10), 有
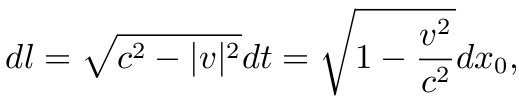
在不引起混淆时, 特别在公式中, v 也指 |v|.
对刚才得到的公式

积分
得

因此, 特别的, 当 v=0 时, 即粒子关于空间坐标系 (x) 不动, 则其 proper time 是
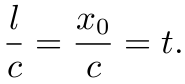
下面我们来推导 Lorentz 变换的具体形式.
为简单起见, 考虑 R21,1 上的 Lorentz 变换.
R21,1 上的度量为![]()
度量矩阵为
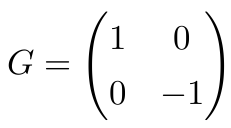
在 Lorentz 变换
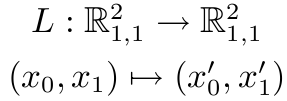
之下, 要求度量为
度量矩阵仍为 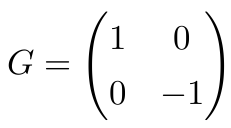
既然是线性变换, 我们可设
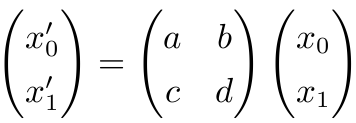
记 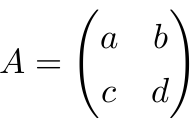
则推出 G=ATGA.
证明:
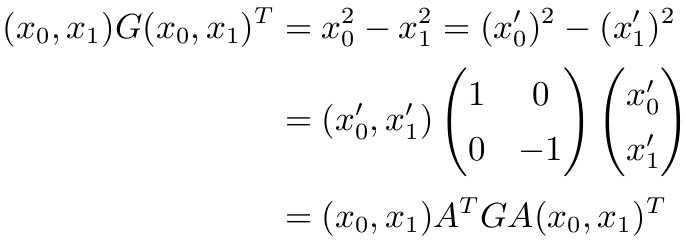
因而由 (x0,x1) 的任意性, 得 G=ATGA.
Q.E.D
由 G=ATGA, 且
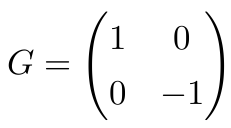
所以 |G|=-1, 且推出 |A|=±1.
并且还可以进一步计算出 a,b,c,d 的关系.
代入 G=ATGA, 计算得
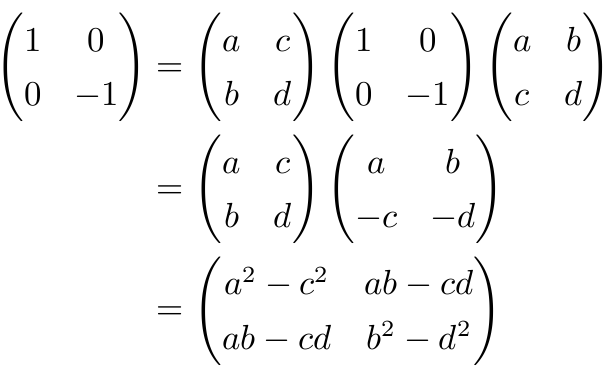
从而推出
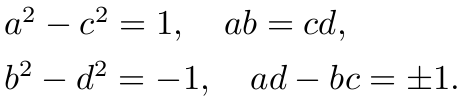
显见 a≠0, 若令 β=c/a, 则
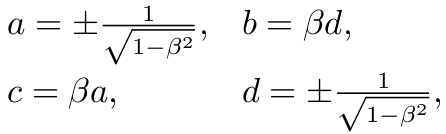
故 A 形如

令 β=tanhψ, 则
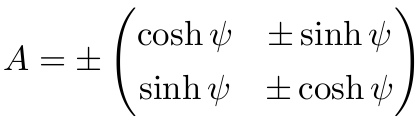
由于 |A|=±1, 故 A 只能是下列四种形式之一:
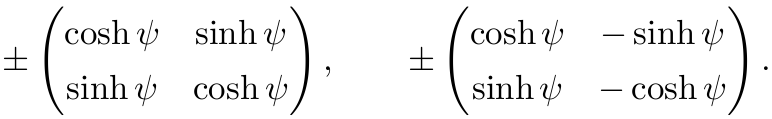
欧氏空间的正交变换群有两个连通分支;
而这里伪欧氏空间 R21,1 保持原点不动的等距群 O(1,1) 有四个连通分支.
Lorentz 变换是保距的,
对于 |ξ|2=const. 的集合, 变换后保持不变.
因此特别的对于光锥和 hyperbola (|ξ|2=1 的集合), Lorentz 变换作用后是不变的.
Hyperbola
现在来看如何导出 Lorentz 变换的公式.
我们讲到 Minkowski 空间中的 Lorentz 变换是指
其中空间坐标系 (x') 以相对于空间坐标系 (x) 以速度 v 作匀速运动.
不妨是沿着 x1 方向运动的, x'2=x2, x'3=x3.
由前面的讨论, 这样的保距变换一定是线性的, 而且还求出了其矩阵形式.
具体的,
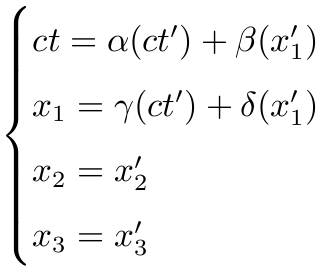
其中
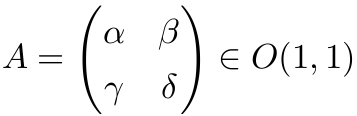
若速度 v→0, 则该 Lorentz 变换应该是恒同变换.
因此, A 应位于 O(1,1) 的单位元连通分支中, 也即 A 必形如
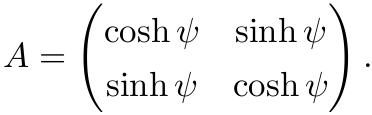
从而
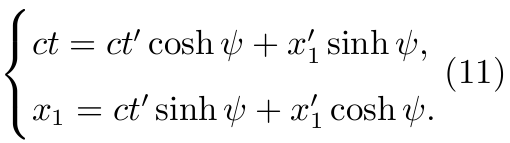
我们特别的来考察 (x') 空间坐标系中原点在相对于参照系 (ct,x1,x2,x3) 的运动.
假设 O'(t') 是空间坐标系 (x') 在时刻 t' 时在自身参照系 (ct',x'1,x'2,x'3) 中的位置.
则 O'(t') 在自身参照系中是沿 ct' 轴在运动, x'1 始终为 0.
将 x'1=0 代入左式, 得
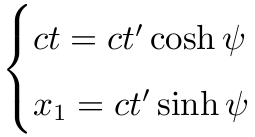
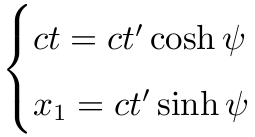
两式相除, 得
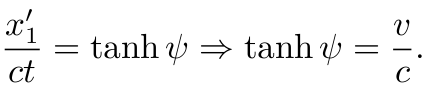
从而有
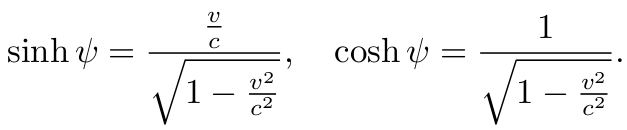
将它们代入(11), 得
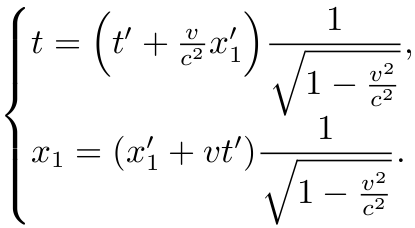
我们看到, 上式中当 v/c→0 时,
Lorentz 变换退化为 Galileo 变换.
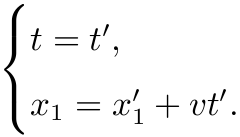
也就是说当 v/c <<1, Lorentz 变换近似等于经典变换.
但当 v 接近光速时, 情况则会有很大不同.
谢 谢!