首页
— A First Course in Database systems —
Haifeng Xu
(hfxu@yzu.edu.cn)
This slide is based on Jeffrey D. Ullman's work, which can be download from his website.
代数, 关系代数, 关系
- 域 $\mathbb{K}$ 上的代数(algebra)
- 设 $A$ 是 域 $\mathbb{K}$ 上的一个向量空间, 并且 $A$ 上有二元运算 $A\times A\rightarrow A$. 如果映射 $A\times A\rightarrow A$ 是双线性的, 则称 $A$ 是域 $\mathbb{K}$ 上的一个代数.
这里 $A$ 中的元素称为操作数(operand), $\times$ 称为操作符(operator)
- 关系(relation)
- 设 $A$, $B$ 是两个集合, $r$ 是笛卡尔积 $A\times B$ 的一个子集, 则称 $r$ 是一个(二元)关系. 同理可以定义多元关系.
- 关系代数(relational algebra)
- 设 $A$ 是 域 $\mathbb{K}$ 上的一个代数, 如果其操作数是关系(relations), 或者代表操作数的变量是关系, 则称
$A$ 是关系代数.
关系代数中的操作符被定义为用来完成数据库中各种关系之间运算的映射.
也就是说, 这些操作符的集合成为了数据库的查询语言(query language).
主要的关系代数操作符
- 并(union)、交(intersection)、差(difference)
- 与通常的集合运算不同, 这里要求两个操作数具有相同的关系模式.
- 选择(selection): 取出某些行.
- 投影(projection): 取出某些列.
- 乘积(products) 和连接(joins): 关系的组合.
- 重命名(renaming)关系和属性.
Selection
- $R_1:=\sigma_C(R_2)$
- $C$ 是关于 $R_2$ 中属性的条件 (即 if 语句中的内容)
- $R_1$ 等于关系 $R_2$ 中所有满足条件 $C$ 的元组集合.
例子: Selection
关系 Sells:
| bar |
beer |
price |
| Joe's |
Bud |
2.50 |
| Joe's |
Miller |
2.75 |
| Sue's |
Bud |
2.50 |
| Sue's |
Miller |
3.00 |
$\text{JoeMenu}:=\sigma_{\text{bar="Joe's"}}(\text{Sells})$
| bar |
beer |
price |
| Joe's |
Bud |
2.50 |
| Joe's |
Miller |
2.75 |
投影(Projection)
投影(Projection)操作用来从关系 $R$ 生成一个新的关系, 这个关系只包含原来关系 $R$ 中的部分列.
$R_1:=\pi_{L}(R_2)$
- $L$ 是关系 $R_2$ 的模式(schema)中的某些属性组.
- 通过扫描 $R_2$ 的每一个元组(tuple), 根据 $L$ 中指定的属性组,
按照指定顺序, 从 $R_2$ 的元组中生成对应属性的新元组.
- 如果有重复元组, 则排除.
例子: Projection
关系 Sells:
| bar |
beer |
price |
| Joe's |
Bud |
2.50 |
| Joe's |
Miller |
2.75 |
| Sue's |
Bud |
2.50 |
| Sue's |
Miller |
3.00 |
$\text{Prices}:=\pi_{\text{beer,price}}(\text{Sells})$
| beer |
price |
| Bud |
2.50 |
| Miller |
2.75 |
| Miller |
3.00 |
Extended Projection
使用同样的投影操作 $\pi_L$, 这里允许列表 $L$ 包含关于属性的任意表达式:
- 属性之间的算术运算, 如: $A+B\rightarrow C$
- 相同的属性可以多次出现.
例子: Extended Projection
R
$\pi_{A+B\rightarrow C,A,A}(R)$
| C |
$A_1$ |
$A_2$ |
| 3 |
1 |
1 |
| 7 |
3 |
3 |
乘积(Product)
$R_3:=R_1\times R_2$
- $R_3=\{(a,b)\mid a\in R_1,\ b\in R_2\}$
- $R_3$ 的模式就是在 $R_1$ 的模式基础上, 按顺序添加 $R_2$ 的模式.
- 如果两个关系 $R_1$, $R_2$ 有同名属性 $A$, 则用关系名加上属性名来区分, 如 $R_1.A$, $R_2.A$.
例子: Product
$R_3:=R_1\times R_2$
$R_3$
| A |
$R_1.B$ |
$R_2.B$ |
$C$ |
| 1 |
2 |
5 |
6 |
| 1 |
2 |
7 |
8 |
| 1 |
2 |
9 |
10 |
| 3 |
4 |
5 |
6 |
| 3 |
4 |
7 |
8 |
| 3 |
4 |
9 |
10 |
Theta 连接($\theta$-Join)
$R_3:=R_1\bowtie_C R_2$
- 先取乘积 $R_1\times R_2$
- 然后应用 $\sigma_C$ 得到 $R_3$.
对于 $\sigma$, $C$ 可以是任何布尔值的条件.
- 这个操作符以前旧的版本仅允许 $A\ \theta\ B$, 其中 $\theta$ 指 $=,\,< $ 等等, 因此命名为 $\theta$-连接.
例子: Theta Join
Sells
| bar |
beer |
price |
| Joe's |
Bud |
2.50 |
| Joe's |
Miller |
2.75 |
| Sue's |
Bud |
2.50 |
| Sue's |
Miller |
3.00 |
Bars
| name |
addr |
| Joe's |
Maple St. |
| Sue's |
River Rd. |
$\text{BarInfo}:=\text{Sells}\bowtie_{\text{Sells.bar=Bars.name}}\text{Bars}$
BarInfo
| bar |
beer |
price |
name |
addr |
| Joe's |
Bud |
2.50 |
Joe's |
Maple St. |
| Joe's |
Miller |
2.75 |
Joe's |
Maple St. |
| Sue's |
Bud |
2.50 |
Sue's |
River Rd. |
| Sue's |
Coors |
3.00 |
Sue's |
River Rd. |
自然连接(Natural Join)
自然连接(Natural Join)
- 是对于两个关系中共同的属性, 且此属性有相同的值进行配对;
- 相同属性仅投影其中一个.
记为 $R_3:=R_1\bowtie R_2$.
例子: Natural Join
Sells
| bar |
beer |
price |
| Joe's |
Bud |
2.50 |
| Joe's |
Miller |
2.75 |
| Sue's |
Bud |
2.50 |
| Sue's |
Miller |
3.00 |
Bars
| name |
addr |
| Joe's |
Maple St. |
| Sue's |
River Rd. |
$\text{BarInfo}:=\text{Sells}\bowtie\text{Bars}$
注意: 为使自然连接能成功, $\text{Bars.name}$ 应重命名为 $\text{Bars.bar}$
BarInfo
| bar |
beer |
price |
addr |
| Joe's |
Bud |
2.50 |
Maple St. |
| Joe's |
Miller |
2.75 |
Maple St. |
| Sue's |
Bud |
2.50 |
River Rd. |
| Sue's |
Coors |
3.00 |
River Rd. |
重命名(Renaming)
为了有效地管理由关系代数生成的结果关系的属性名字, 通常会引进一个重命名操作.
- $R_1:=\rho_{R_1(A_1,\ldots,A_n)}(R_2)$ 表示对关系 $R_2$ 重新命名, 并且属性名分别重命名为 $A_1,\ldots,A_n$.
- 重命名后的关系 $R_1$ 与原关系 $R_2$ 具有完全相同的元组.
- 简记为 $R_1(A_1,\ldots,A_n):=R_2$
- 如果属性名不改变, 则简记为 $R_1=\rho_{R_1}(R_2)$, 或 $R_1:=R_2$.
例子: Renaming
Bars
| name |
addr |
| Joe's |
Maple St. |
| Sue's |
River Rd. |
$\text{R}(\text{bar},\text{addr}):=\text{Bars}$
R
| bar |
addr |
| Joe's |
Maple St. |
| Sue's |
River Rd. |
建立复杂的表达式(Building complex expressions)
利用圆括号及优先级规则(precedence rules)将各操作符(算符)结合起来.
三种记号, 与算术中的一样:
- 赋值语句序列(Sequences of assignment statements).
- 具有多个运算符的表达式(Expressions with several operators).
- 表达式树(Expression trees).
赋值语句序列(Sequences of assignment statements)
- 建立临时的关系名.
- 通过为关系提供属性列表, 可以暗示重命名. (Renaming can be implied by giving relations a list of attributes.)
- Example: $R_3:=R_1\bowtie_C R_2$ 可以写为
$R_4:=R_1\times R_2$
$R_3:=\sigma_C(R_4)$
单赋值语句的表达式(Expressions in a single assignment)
- Example: $\theta$-连接 $R_3:=R_1\bowtie_C R_2$ 可以写为
$R_3:=\sigma_C(R_1\times R_2)$
- 关系算符的优先级
- $[\sigma,\ \pi,\ \rho]$ (最高优先级)
- $[\times,\ \bowtie]$
- $\cap$
- $[\cup,\ -]$
表达式树(Expression trees)
- 叶子是操作数(或者是变量或者是常数, 它们都取关系为值).
- 内部节点是操作符, 作用在它们的子节点上.
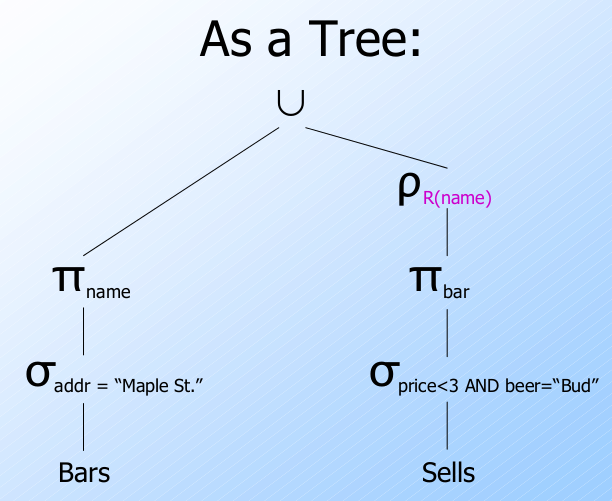
例子: Tree for a query
对于关系 $\text{Bars}(name,addr)$ 和 $\text{Sells}(bar,beer,price)$,
找出位于在 Maple St. 或 Bud 啤酒售价小于 3 美元的酒吧.
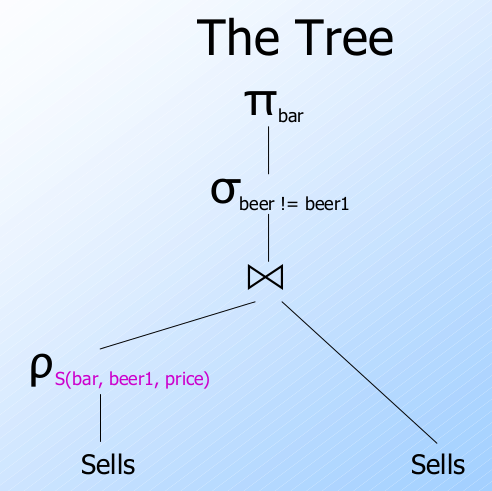
例子: Self-Join
对于关系 $\text{Sells}(bar,beer,price)$,
找出正出售相同价格的两种品牌啤酒的酒吧.
策略(Strategy)
- 通过重命名, 得到关系 $\text{Sells}$ 的一个拷贝, 如 $\text{S}(bar,beer1,price)$.
- $\text{Sells}$ 和 $\text{S}$ 的自然连接产生一个新的关系 $(bar,beer,beer1,price)$.
其中的元组是出售价格相同的两种啤酒的酒吧.
- 但最后必须排除品牌相同的啤酒, 并且投影到属性 $bar$.
Schemas for Results
并(union), 交(intersection), 差(difference)
两个操作数(这里是关系)的模式(schema)必须相同, 所得结果也使用该模式.
选择(selection)
所得结果的模式与操作数的模式相同.
投影(projection)
投影所列出的属性列告诉我们所得结果的模式.
乘积(product)
乘积的模式是两个关系的属性包. 如果遇到属性重名, 则在属性名前加关系名来区分. 如 $\text{R}.A$ 代表关系 $\text{R}$ 的属性 $A$ 等等.
$\theta$-连接(Theta-join)
与乘积一样.
自然连接(Natural Join)
两个关系的属性的并集.
重命名(Renaming)
重命名操作符详细指出了模式.
基于包的关系代数(Relational algebra on bags)
包(bag), 或称多集(multiset)
包(bag)不是严格意义上的集合, 它允许其中的元素可以重复, 并且可以重复不止一次.
例子
- $\{1,2,1,3\}$ 是一个包(bag).
- $\{1,2,3\}$ 也是一个包(bag). 但同时也是一个集合.
为什么使用包?
为什么使用包?
- SQL, 关系数据库最重要的查询语言, 实际上是一种包语言.
- 某些操作, 如投影, 在包上的效率远大于在集合上的效率.
- 商业 DBMS 实现的关系都是包而不是集合.
包上的操作(operations on bags)
包上的操作
- Selection, 应用于每个元组, 因此它作用在包上的效果与作用在集合上的效果是一样的.
- Projection, 也是应用于每个元组, 但作为包操作符, 不必删除重复的元组.
- Products 和Joins, 是针对每对元组进行操作, 因此包中的重复元组对此没有影响.
例子: Bag selection
Bag selection
$\text{R}$
| A |
B |
| 1 |
2 |
| 5 |
6 |
| 1 |
2 |
$\sigma_{A+B<5}(\text{R})$
| A |
B |
| 1 |
2 |
| 1 |
2 |
例子: Bag projection
Bag projection
$\text{R}$
| A |
B |
| 1 |
2 |
| 5 |
6 |
| 1 |
2 |
$\pi_{A}(\text{R})$
| A |
| 1 |
| 5 |
| 1 |
例子: Bag product
Bag product
$\text{R}$
| A |
B |
| 1 |
2 |
| 5 |
6 |
| 1 |
2 |
$\text{R}\times\text{S}$
| A |
R.B |
S.B |
C |
| 1 | 2 | 3 | 4 |
| 1 | 2 | 7 | 8 |
| 5 | 6 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 1 | 2 | 3 | 4 |
| 1 | 2 | 7 | 8 |
例子: Bag $\theta$-Join
Bag $\theta$-Join
$\text{R}$
| A |
B |
| 1 |
2 |
| 5 |
6 |
| 1 |
2 |
$R\bowtie_{R.B < S.B}S$
| A |
R.B |
S.B |
C |
| 1 | 2 | 3 | 4 |
| 1 | 2 | 7 | 8 |
| 5 | 6 | 7 | 8 |
| 1 | 2 | 3 | 4 |
| 1 | 2 | 7 | 8 |
包的并、交、差运算
若元组 $t\in R$, $t\in S$, 且 $t$ 在 $R$, $S$ 中出现的次数分别为 $m,n$ 次(这里 $m$ 和 $n$ 均是非负整数), 则
- $t$ 在 $R\cup S$ 中出现 $m+n$ 次.
- $t$ 在 $R\cap S$ 中出现 $\min\{m,n\}$ 次.
- $t$ 在 $R-S$ 中出现 $\max\{m-n,0\}$ 次.
Bag union
两个包关系的并操作, 指将一个关系的所有元组简单地复制到另一个关系, 而不必消除重复元组.
\[\{1,2,1\}\cup\{1,1,2,3,1\}=\{1,1,1,1,1,2,2,3\}\]
Bag intersection
\[\{1,2,1,1\}\cap\{1,2,1,3\}=\{1,1,2\}\]
Bag difference
\[\{1,2,1,1\}-\{1,2,3\}=\{1,1\}\]
Bag laws != set laws
Beware: Bag laws != set laws
某些(不是全部)关于集合的代数定律对于包来说不再成立.
Example
并的交换律 $R\cup S=S\cup R$ 对于包依旧成立.
某些集合运算法则对于包失效
- 集合的并操作是幂等的(idempotent), 即 $S\cup S=S$.
- 然而若 $S$ 是包, 且 $x\in S$ 出现 $n$ 次, 则 $x$ 在 $S\cup S$ 中将出现 $2n$ 次.
- 因此, 一般的, $S\cup S!=S$. 如 $\{1\}\cup\{1\}=\{1,1\}!=\{1\}$.
另一个例子是集合差对于并的分配律
- $(R\cup S)-T=(R-T)\cup(S-T)$.
- 假设关系 $R,S,T$ 中均有元组 $t$, 且没有重复. 如果上面进行的是包操作, 则 $(R\cup S)-T$ 中仍含有 $t$, 而右边则不含 $t$.
End
Thanks very much!
This slide is based on Jeffrey D. Ullman's work, which can be download from his website.


