首页
UML(Unified Modeling Language)
ODL(Object Definition Language)
Haifeng Xu
(hfxu@yzu.edu.cn)
This slide is based on Jeffrey D. Ullman's work, which can be download from his website.
面向对象的 DBMS
面向对象的 DBMS
Standards group: ODMG=Object Data Management Group.
“Operational Database Management Systems” (ODBMS)
ODL=Object Definition Language. 与 SQL 中的 CREATE TABLE 类似.
OQL=Object Query Language. 试图将 SQL 移植到 OO 框架中.
Framework - (1)
Framework - (1)
ODMG 希望 OO-DBMS 的供应商能够提供像 C++ 那样的面向对象的语言, 并具有扩展(OQL), 使得程序员可以在数据库和“宿主语言”之间进行数据的无缝传输.
Framework - (2)
Framework - (2)
ODL 是用于定义持久化(persistent)的类, 其对象永久存储在数据库中.
- ODL 类看上去像二元联系中的实体集, 只不过多了方法(methods).
- ODL 类的定义是扩展的面向对象宿主语言(OO host language)的一部分.
ODL 概述
ODL 概述
ODL(Object Definition Language, 对象定义语言)是一种基于文本的使用面向对象术语来描述数据库结构的语言.
与 UML 一样, 类是 ODL 中的核心概念. 就像 UML 类一样, ODL 中的类具有名字、属性和方法. “联系”与 UML 的“关联”类似, 但是在 ODL 中“联系”不是一个独立的概念, 而是可以作为特征的附加成员嵌入到类中.
一个类的声明包括:
- 这个类的名字(类名)
- 关键字声明(可选)
- 元素声明. 这里元素可以是属性(attribute)、联系(relationship)或方法(method)
ODL 中一个最简单的类声明形式如下:
class <name> {
<list of properties>
};
这里关键字 class 后面跟着类的名字和一个花括号括起来的特征列表. 特征(properties)可以是属性(attribute)、联系(relationship)或方法(method).
各特征之间使用分号(semicolon)隔开.
ODL 中的属性
ODL 中的属性
最简单的特征是属性(attribute). 在 ODL 中, 属性不必为整型或字符串等简单类型. ODL 有一个类型系统, 它允许构建结构类型或集合类型.
例如,
- 属性 address 可以是由街道、城市和邮政编码等字段构成的结构类型.
- 属性 phone 可以是字符串集合作为类型, 甚至可以是更为复杂的类型.
在类声明中, 属性是由关键字 attribute、属性的类型和名字表示的.
例如, Movie 类的 ODL 声明
class Movie {
attribute string title;
attribute integer year;
attribute integer length;
attribute enum Genres {drama, comedy, sciFi, teen} genre;
};
这里最后一个属性 genre 是枚举(enum)类型 Genres, 花括号中的列表列出了此枚举类型 Genres 的取值. 枚举类型必须有一个名字.
属性和联系的声明(Attribute and Relationship Declarations)
属性和联系的声明(Attribute and Relationship Declarations)
属性(通常)是指带有某种(不涉及类的)类型的元素.
attribute <type> <name>;
relationship <type> <name>
inverse <relationship>;
联系(relationships)连接某个对象到从属于某个类的一个或多个对象.
ODL 联系是在类的声明里面通过关键字 relationship、类型和联系名字来声明.
联系类型描述了类的一个单个对象与这个联系连接. 典型地, 这个类型可以是另外一个类(如果联系是多对一的)或者一个集合类型(如果联系是一对多或者多对多).
例子 4.48
假设要给例 4.46 中的 Movie 类声明增加一个属性: 一组影星. 更明确地说, 是要求每个 Movie 对象都与一组 Star 对象(该电影的影星)连接. 表达两个类 Movie 和 Star 之间连接的最好方式是使用联系(relationship). 该联系可以在 Movie 类声明中用以下代码行实现:
relationship Set<Star> stars;
inverse <relationship>;
这样, 在每个 Movie 类的对象中, 都有一组对 Star 对象的引用. 这组引用命名为 stars.
反向联系(Inverse Relationships)
反向联系(Inverse Relationships)
假设类 C 有一个联系(relationship) R连接C到D.
于是类 D 必存在到类 C 的某个联系 S.
R 和 S 必须是真正的逆.
如果对象 d 经由联系 R 连接到对象 c, 则 c 必定经 S 连接到 d.
例子: 属性和联系
例子: 属性和联系
class Bar {
attribute string name;
attribute string addr;
relationship Set<Beer> serves inverse Beer::servedAt;
}
class Beer {
attribute string name;
attribute string manf;
relationship Set<Bar> servedAt inverse Bar::serves;
}
The type of relationship serves
is a set of Beer objects.
The :: operator connects
a name on the right to the
context containing that
name, on the left.
关系的类型
关系的类型(Types of Relationships)
关系的类型是下面几种类型之一:
- 一个类, 例如 Bar. 若是这样, 具有此关系的对象只能联系到一个 Bar 对象.
- Set<Bar>: 此对象连接到一个 Bar 对象集.
- Bag<Bar>, List<Bar>, Array<Bar>: 此对象连接到装有 Bar 对象的一个包(Bag), 链表(List) 或数组(array).
关系的多重性
Multiplicity of Relationships
所有 ODL 关系都是 binary 的.
多对多的关系(many-many relationship)以及其反向关系具有 Set<...> 类型.
多对一的关系(many-one relationship)对于 "one" 具有 Set<...> 类型, 而多的一方("many")只是class类型.
一对一联系在两个方向上都是 class 类型.
例子: 多重性
例子: 多重性(Multiplicity)

另一个多重性例子
另一个多重性例子

处理多路关系
处理多路关系(Coping with Multiway Relationships)
ODL 不支持 3-路或更高路的关系.
我们必须通过一个"连接"类(connecting class)模仿多路关系, 其对象代表了我们希望通过多路关系连接的一大堆对象.
连接类(Connecting Classes)
连接类(Connecting Classes)
To do ...
- Drinkers1(name,addr)
- 在 4NF 中, 仅有的函数依赖是 $\text{name}\rightarrow\text{addr}$.
- Drinkers2(name,phones,beersLiked)
- 这个子关系不属于 4NF. 因为有多值依赖 $\text{name}\rightarrow\rightarrow\text{phones}$ 和 $\text{name}\rightarrow\rightarrow\text{beersLiked}$ 存在. 并且没有函数依赖, 因此所有这三个属性构成了这个子关系的键.
例子: 分解子关系 Drinkers2
例子: 分解子关系 Drinkers2
刚才两个 MVD $\text{name}\rightarrow\rightarrow\text{phones}$ 和 $\text{name}\rightarrow\rightarrow\text{beersLiked}$ 告诉我们要将关系 Drinkers2 分解为:
- Drinkers3(name,phones)
- Drinkers4(name,beersLiked)
MVD's+FD's 的原因
MVD's+FD's 的原因
问题: 对于关系 R, 给定 MVD 集合和 FD 集合. 某个 FD 或某个 MVD 是否也在 R 上成立.
解决办法: 利用图例去发现给定集合的所有推断, 去检查是否可以推断出目标依赖.
为什么我们要关注
为什么我们要关注
- 4NF 技术上需要一个 MVD 违例.
- 需要从给定的 FD's 和 MVD's(它们可能自身并不违反 4NF)去推断违反 4NF 的 MVD's
- 当我们分解时, 我们需要将 FD's+MVD's 作投影.
例子: 追踪含有 MVD's+FD's 的图例
例子: 追踪含有 MVD's+FD's 的图例
为应用 FD, 和以前一样, 要使得符号相等.
To apply an MVD, generate one or both of the tuples we know must also be in the relation represented by the tableau.
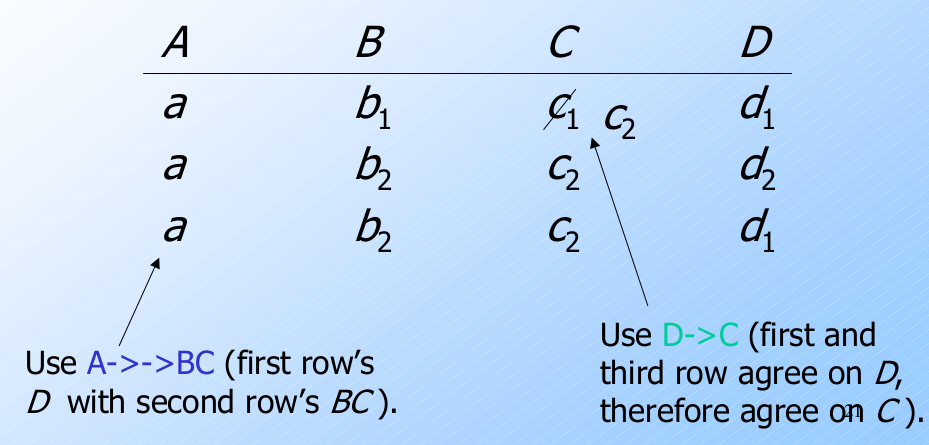
我们将证明: 如果有多值依赖 $A\rightarrow\rightarrow BC$ 和函数依赖 $D\rightarrow C$, 则可推断出 $A\rightarrow C$.
$A\rightarrow C$ 的图例
$A\rightarrow C$ 的图例
目标是证明: $c_1=c_2$.
例子: MVD 的传递规则(Transitive Law for MVD's)
例子: MVD 的传递规则(Transitive Law for MVD's)
若 $A\rightarrow\rightarrow B$ 且 $B\rightarrow\rightarrow C$, 则 $A\rightarrow\rightarrow C$.
- 如果数据库模式是 $ABC$, 则根据多值依赖的互补规则, 上面的断言显然成立.
- 但这个断言对于其他数据模式也是成立的. 比如我们考虑关系 $R(ABCD)$.
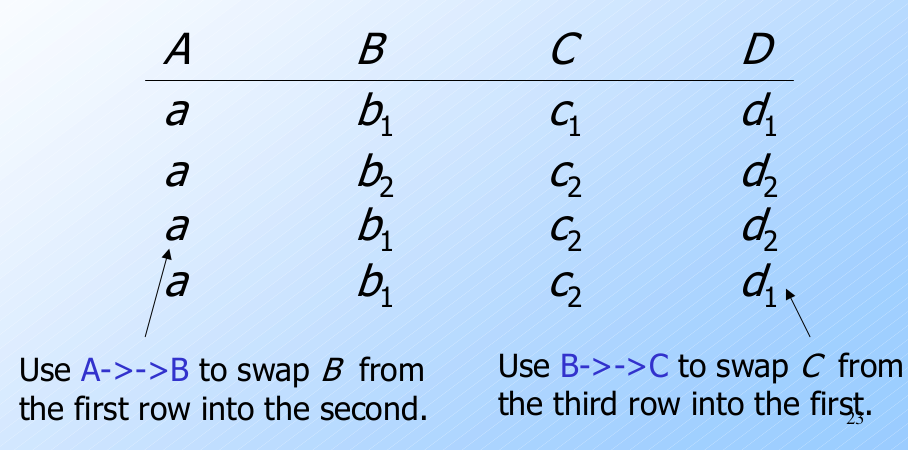
$A\rightarrow\rightarrow C$ 的图例
$A\rightarrow\rightarrow C$ 的图例
目标: 推断存在元组 $(a, b_1, c_2, d_1)$.
推断 MVD's+FD's 的规则
推断 MVD's+FD's 的规则
从一个具有两行的图例来说明.
- 这些行在要推断的依赖的左边属性集上取值是一致的.
- 并且它们在其他属性集上不一致.
- 对于取值一致的, 用没有下标的字母表示, 如果不一致则使用下标.
推断: 应用函数依赖(Inference: Applying a FD)
推断: 应用函数依赖(Inference: Applying a FD)
应用函数依赖 $X\rightarrow Y$. 找出在属性集 $X$ 上一致的行, 迫使它们在属性集 $Y$ 上取值也一致.
- 将一个变量用另一个替代.
- 若被替换的变量是目标元组的一部分, 则也替换.
推断: 应用多值依赖(Inference: Applying a MVD)
推断: 应用多值依赖(Inference: Applying a MVD)
应用多值依赖 $X\rightarrow\rightarrow Y$. 对于在属性集 $X$ 上取值相同的两行,
- 在图例中加入那些通过交换此两行在 $Y$ 部分而得到那些行.
- 实际上, 就是将 $Y$ 属性组和剩余属性组 $R-X-Y$ 上的值作笛卡尔积.
Inference: Goals
Inference: Goals
为测试 $U\rightarrow V$ 是否成立, 我们接着察看 $V$ 属性组上的两个变量是否相同.
如果我们测试的是多值依赖 $U\rightarrow\rightarrow V$, 我们察看图例中的一行是否是原来的那行, 即是通过交换属性组 $V$ 上的值得到的.
Inference: Endgame
Inference: Endgame
应用所有给定的 FD's 和 MVD's, 直到我们不再改变图例为止.
如果我们达到目的, 则依赖性被推出.
否则, 所得到的最后的图例是一个反例.
- 它满足所有给定的依赖关系.
- 最初的两行违反目标依赖.
End
Thanks very much!
This slide is based on Jeffrey D. Ullman's work, which can be download from his website.



