首页

多值依赖

第四范式
Reasoning About FD's + MVD's

Haifeng Xu

(hfxu@yzu.edu.cn)

This slide is based on the book of Jeffrey D. Ullman and his slide, which can be download from his website.

多值依赖(MVD)的定义

多值依赖(Multivalued dependency)是两个属性或属性集合之间相互独立的断言. 它是广义的函数依赖.

在某种意义上, 每个FD意味着一个相应的多值依赖. 但是仍然存在有不能用FD解释的属性集合相互独立的情况.

这里我们将说明引起多值依赖的原因和在数据库模式设计中如何使用多值依赖.

属性独立及随之产生的冗余

在设计关系模式时, 有时会有一些偶然的情况, 即某个模式属于 BCNF, 但在相应的关系中还有与 FD 无关的冗余存在.

在 BCNF 模式中最常见的导致冗余的情形是试图把键的两个或多个集合值属性置于同一个关系中.

例 3.28

本例中, 主要存储的对象是影星. 假设影星有多处地址, 地址包括街道(street)和城市(city)两部分.

地址集合(street and city)是关系要存储的一个集合值属性子集.

另一个要存储的集合值属性子集是该影星出演电影的名称(title)和发行年份(year).

关系的模式和所包含的函数依赖关系

因此此关系的模式是 $R(name, street, city, title, year)$

函数依赖集合为空集, 因为不存在非平凡的函数依赖. (注意 $street\not\rightarrow city$, $title\not\rightarrow year$.)

因此关系不存在BCNF违例, 但是数据明显有冗余.


name	street	city	title	year
C. Fisher	123 Maple St.	Hollywood	Star Wars	1977
C. Fisher	5 Locust Ln.	Malibu	Star Wars	1977
C. Fisher	123 Maple St.	Hollywood	Empire Strikes Back	1980
C. Fisher	5 Locust Ln.	Malibu	Empire Strikes Back	1980
C. Fisher	123 Maple St.	Hollywood	Return of the Jedi	1983
C. Fisher	5 Locust Ln.	Malibu	Return of the Jedi	1983

表中给出了 Carrie Fisher 的两个假设的地址和她的三部著名的电影. 没有理由只把某个地址和某部影片关联, 而不与另一部影片关联. (除非特别指明她在拍某部电影时, 一直住在其中某个地址.)

因此, 表达影星的地址和电影相互独立的唯一途径是把地址和电影的各种组合(这里总共是 $2\times 3=6$ 种)都罗列出来. 但是这样的组合明显包含数据冗余.

该关系的键是由所有五个属性构成的唯一的键: $(\underline{name}, \underline{street}, \underline{city}, \underline{title}, \underline{year})$.

MVD 的定义

多值依赖(multivalued dependency, MVD)的定义

关系 $R$ 上的一个多值依赖(multivalued dependency)(MVD): $X\rightarrow\rightarrow Y$, 是指:
若 $R$ 的两个元组在属性组 $X$ 上的值一致, 则它们在属性组 $Y$ 上的取值(可看成是向量)可以互相交换, 并且交换后得到的两个元组仍在这个关系中.

换句话说, 对每个 $X$ 上的值(向量值), $Y$ 上的值(向量值)独立于 $R-X-Y$ 上的值(向量值).

课本上的定义

多值依赖(MVD)是指在关系 $R$ 中, 当给定某个属性集合的值时, 存在另外一组属性集合, 该组属性的值与关系中所有其他属性的值无关(即该组属性的值独立于关系中所有其他属性的值).

精确地说, 若给定关系 $R$ 中属于属性子集 $\mathcal{A}$ 的各属性的值, 存在一个属性子集 $\mathcal{B}$, 其中属性的值独立于 $R$ 中既不属于 $\mathcal{A}$ 也不属于 $\mathcal{B}$ 的属性集合的值, 则称 MVD \[ A_1 A_2\cdots A_n\rightarrow\rightarrow B_1 B_2\cdots B_m \] 在关系 $R$ 中成立.

更准确的说法是: 若要 MVD 成立, 则对于关系 $R$ 中每对在属性组 $\mathcal{A}$ 上一致的元组 $t$ 和 $u$, 存在 $R$ 中满足下列条件的元组 $v$:

在属性组 $\mathcal{A}$ 上的取值(向量值)与 $t$ 和 $u$ 相同; (即 $v\Bigr|_{\mathcal{A}}=t\Bigr|_{\mathcal{A}}=u\Bigr|_{\mathcal{A}}$)
在属性组 $\mathcal{B}$ 上的取值(向量值)与 $t$ 相同; (即 $v\Bigr|_{\mathcal{B}}=t\Bigr|_{\mathcal{B}}$)
在关系$R$ 中不属于 $\mathcal{A}$ 和 $\mathcal{B}$ 的所有其他属性上的取值与 $u$ 相同. (即 $v\Bigr|_{\mathcal{R}-\mathcal{A}-\mathcal{B}}=u\Bigr|_{\mathcal{R}-\mathcal{A}-\mathcal{B}}$)

上面定义中 $t$ 和 $u$ 交换一下, 存在 $w$ 满足:

$w\Bigr|_{\mathcal{A}}=u\Bigr|_{\mathcal{A}}=t\Bigr|_{\mathcal{A}}$)
$w\Bigr|_{\mathcal{B}}=u\Bigr|_{\mathcal{B}}$)
$w\Bigr|_{\mathcal{R}-\mathcal{A}-\mathcal{B}}=t\Bigr|_{\mathcal{R}-\mathcal{A}-\mathcal{B}}$)

平凡 MVD

平凡MVD(trivial MVD)

例1

若关系 R 的所有属性为 $\{A_1,A_2,\ldots,A_n,B_1,B_2,\ldots,B_m\}$. 则 $A_1A_2\cdots A_n\rightarrow\rightarrow B_1B_2\cdots B_m$ 在 R 上成立.

证明: 如果选取两个在属性集 $\mathcal{A}:=\{A_1,A_2,\ldots,A_n\}$ 上一致的元组 $t_1,t_2$, 互换其在属性组 $\mathcal{B}:=B_1,B_2,\ldots,B_m$ 上的分量值. 即, 若记 $t_1=(a,b_1)$, $t_2=(a,b_2)$. 这里 $a=t_1|_{\mathcal{A}}=t_2|_{\mathcal{A}}$, $b_i=t_i|_{\mathcal{B}}$. 互换 $b_1$ 和 $b_2$, 得到的元组如果记为 $u_1, u_2$. 则它们还是原来的元组, $u_1=t_2$, $u_2=t_1$, 只是顺序倒过来了. 因此是平凡的MVD.

例1

如果 $\mathcal{B}\subset\mathcal{A}$, 则 \[ \mathcal{A}\rightarrow\rightarrow\mathcal{B} \] 是一个平凡的MVD.

证明. 略.

MVD 的传递规则

设关系 $R(\mathcal{R})$ 包含了属性组 $\mathcal{A}$, $\mathcal{B}$, $\mathcal{C}$. 且有 MVDs \[ \mathcal{A}\rightarrow\rightarrow\mathcal{B},\qquad \mathcal{B}\rightarrow\rightarrow\mathcal{C} \] 则 $\mathcal{A}\rightarrow\rightarrow\mathcal{C}-\mathcal{A}$ 是关系 $R(\mathcal{R})$ 上的一个 MVD.

例子1: MVD

例 3.29: MVD

例 3.29 在关系 $R(name, street, city, title, year)$ 中给出了一个 MVD, 用符号表示是: \[ name\rightarrow\rightarrow street city \]

也就是说, 对于每个影星的姓名、地址构成的集合与影星所演的每部电影都联合出现.

下面举例说明怎样应用MVD的定义.

考虑下面两个元组


name	street	city	title	year
C. Fisher	123 Maple St.	Hollywood	Star Wars	1977
C. Fisher	5 Locust Ln.	Malibu	Empire Strikes Back	1980

假设第一个元组为 $t$, 第二个元组为 $u$, 那么根据 MVD, 关系 $R$ 中必然存在一个 $name$ 为 C. Fisher, $street, city$ 上的取值与 $t$ 相同, 而其他属性 ($title, year$) 与元组 $u$ 取值相同的元组. (此即原来表中第三个元组.)

类似地, 将 $t,u$ 互换, 即 $t$ 为第二个元组, $u$ 为第一个元组. 根据 MVD 可知, 关系 $R$ 中必有 \[ C.\ Fisher | 5\ Locust\ Ln. | Malibu | Star\ Wars | 1977 \]

例子2: MVD

考虑关系 Drinkers(name, addr, phones, beersLiked)

酒客的手机号码独立于他们喜欢的啤酒名称.

$\text{name}\rightarrow\rightarrow\text{phones}$
$\text{name}\rightarrow\rightarrow\text{beersLiked}$

于是, 每一个酒客的电话号码和他所喜欢的啤酒的所有组合都将出现.

这里的重复与 FD 的冗余不同.

$\text{name}\rightarrow\text{addr}$ 是仅有的函数依赖.

根据多值依赖$\text{name}\rightarrow\rightarrow\text{phones}$ 推出的其他元组

如果我们有下面的元组:


name	addr	phones	beersLiked
sue	a	p1	b1
sue	a	p2	b2

则下面这些元组也将出现在关系中.


name	addr	phones	beersLiked
sue	a	p2	b1
sue	a	p1	b2

多值依赖 $X\rightarrow\rightarrow Y$ 的图解

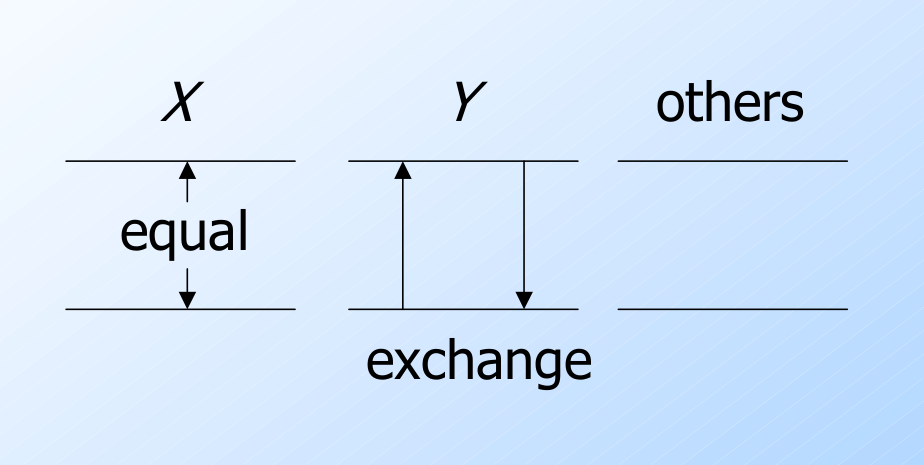
多值依赖的推导

了解什么是平凡 MVD.
MVD 的传递规则.
MVD 不遵循右端分解规则.
FD 升级规则.
互补规则.

前两个之前已经讲过了. 下面给出 MVD 不遵循右端分解规则的一个例子.

MVD 不遵循右端分解规则

例 3.30 考虑之前的关系 $R(name, street, city, title, year)$. 这里存在一个 MVD: \[ name\rightarrow\rightarrow street\ city \]

MVD 的规则

函数依赖可以认为是数学上的映射, 多值依赖可以认为是特殊的多值映射. 因此在这个意义下, 每个函数依赖是一个多值依赖(MVD).

我们从多值依赖的定义去解释一下:

设有函数依赖 $\mathcal{X}\rightarrow\mathcal{Y}$, 对于 $\mathcal{X}$ 部分相同的两个元组, 交换它们在 $\mathcal{Y}$ 部分的值, 事实上, 由于 $\mathcal{X}\rightarrow\mathcal{Y}$, 因此交换后, 并不改变这两个元组.
从而, 交换后的两个“新”元组还是原来那两个, 自然就在该关系中. 故而满足定义, 即成立 MVD $\mathcal{X}\rightarrow\rightarrow\mathcal{Y}$

我们将上面所述称为 FD升级(FD promotion)规则.

FD升级(FD promotion)规则: 每个FD都是MVD. 也就是说, 若 $A_1A_2\cdots A_n\rightarrow B_1B_2\cdots B_m$ 成立, 则 $A_1A_2\cdots A_n\rightarrow\rightarrow B_1B_2\cdots B_m$ 也成立.

证明参考书本P.63.

互补(Complementation): 若有多值依赖 $\mathcal{X}\rightarrow\rightarrow\mathcal{Y}$, 设 $\mathcal{Z}$ 是剩下所有属性构成的属性集, 即 $\mathcal{Z}=\mathcal{R}-\mathcal{X}-\mathcal{Y}$. 则 $\mathcal{X}\rightarrow\rightarrow\mathcal{Z}$.

互补规则实际上是因为 $\mathcal{Y}$ 和 $\mathcal{Z}$ 的地位是相等的.

分裂规则不再成立(Splitting Doesn't Hold)

与 FD 一样, 对于 MVD, 我们不能将它的左边分裂.

但与 FD 不同, 对于 MVD, 我们同样不能分裂右边. 有时我们必须在右边保持若干属性.

例子: 右侧是多属性集(Multiattribute Right Sides)

Drinkers(name,areaCode,phone,beersLiked,manf)

一个酒客可以有多个固定电话号码, 每个固定电话号码可以分解为"区号+电话号码"(areaCode phone).

一个酒客可以喜欢几种啤酒, 每种啤酒的生产厂家都不同.

由于 areaCode phone 组合独立于 beersLiked manf 组合, 因此我们有下面的多值依赖:
$\text{name}\rightarrow\rightarrow\text{areaCode phone}$
$\text{name}\rightarrow\rightarrow\text{beersLiked manf}$

例子数据

下面的数据满足多值依赖的定义:


name	areaCode	phone	beersLiked	manf
Sue	650	555-1111	Bud	A.B.
Sue	650	555-1111	WickedAle	Pete's
Sue	415	555-9999	Bud	A.B.
Sue	415	555-9999	WickedAle	Pete's

但是对于两个在$\text{name}$属性上相同的元组, 我们不能交换 areaCode 列的两个值或 phone 列中两个值. 因此对于这个关系,
$\text{name}\rightarrow\rightarrow\text{areaCode}$ 和 $\text{name}\rightarrow\rightarrow\text{phone}$ 均不成立.

第四范式(Fourth Normal Form)

符合 BCNF 的数据库模式, 如果有多值依赖存在, 则其中的数据冗余是不能去除的.

有一个更强的范式, 称为 4NF. 它在进行数据库模式分解时, (直观地)把 MVD 当作 FD; 但在决定关系的键时, 则不这样直接对待.

4NF 的定义

关系 R 称为是 4NF 的, 如果满足: 只要存在非平凡的多值依赖 $X\rightarrow\rightarrow Y$, 则 $X$ 是超键.

回忆: $X\rightarrow\rightarrow Y$ 是非平凡的 MVD 是指:
1. $Y$ 不是 $X$ 的一个子集.
2. $X$, $Y$ 不包括所有的属性.
注意到超键的定义仍然仅依赖于 FD.

BCNF 对比 4NF

回忆, 每个 FD: $X\rightarrow Y$ 都是一个多值依赖 MVD: $X\rightarrow\rightarrow Y$

于是, 若关系 $R$ 是 4NF 的, 则它当然是 BCNF 的.

因为每个 BCNF 违例是 4NF 违例(当将之转换为 MVD 后).

但是关系 $R$ 可能是 BCNF 但不是 4NF 的, 因为 MVD 对于 BCNF 是不可见的.

Decomposition and 4NF

若 $X\rightarrow\rightarrow Y$ 是关系 $R$ 的一个 4NF 违例, 则我们可以使用类似于 BCNF 的技巧将它分解.

$XY$ 是分解后的其中一个关系模式.
$\mathcal{R}-(Y-X)$ 是另一个关系模式.

例子: 4NF 分解

Drinkers(name,addr,phones,beersLiked)

FD: $\text{name}\rightarrow\text{addr}$

MVD:

$\text{name}\rightarrow\rightarrow\text{phones}$
$\text{name}\rightarrow\rightarrow\text{beersLiked}$

键是 {name,phones,beersLiked}
所有依赖违反了 4NF.

例子: 4NF 分解 -- (2)

例子: 4NF 分解 --(2)

利用 $\text{name}\rightarrow\text{addr}$ 对原关系 Drinkers进行分解.

Drinkers1(name,addr)
- 在 4NF 中, 仅有的函数依赖是 $\text{name}\rightarrow\text{addr}$.
Drinkers2(name,phones,beersLiked)
- 这个子关系不属于 4NF. 因为有多值依赖 $\text{name}\rightarrow\rightarrow\text{phones}$ 和 $\text{name}\rightarrow\rightarrow\text{beersLiked}$ 存在. 并且没有函数依赖, 因此所有这三个属性构成了这个子关系的键.

例子: 分解子关系 Drinkers2

刚才两个 MVD $\text{name}\rightarrow\rightarrow\text{phones}$ 和 $\text{name}\rightarrow\rightarrow\text{beersLiked}$ 告诉我们要将关系 Drinkers2 分解为:

Drinkers3(name,phones)
Drinkers4(name,beersLiked)

MVD's+FD's 的原因

问题: 对于关系 R, 给定 MVD 集合和 FD 集合. 某个 FD 或某个 MVD 是否也在 R 上成立.

解决办法: 利用图例去发现给定集合的所有推断, 去检查是否可以推断出目标依赖.

为什么我们要关注

4NF 技术上需要一个 MVD 违例.
- 需要从给定的 FD's 和 MVD's(它们可能自身并不违反 4NF)去推断违反 4NF 的 MVD's
当我们分解时, 我们需要将 FD's+MVD's 作投影.

例子: 追踪含有 MVD's+FD's 的图例

为应用 FD, 和以前一样, 要使得符号相等.

To apply an MVD, generate one or both of the tuples we know must also be in the relation represented by the tableau.

我们将证明: 如果有多值依赖 $A\rightarrow\rightarrow BC$ 和函数依赖 $D\rightarrow C$, 则可推断出 $A\rightarrow C$.

$A\rightarrow C$ 的图例

目标是证明: $c_1=c_2$.

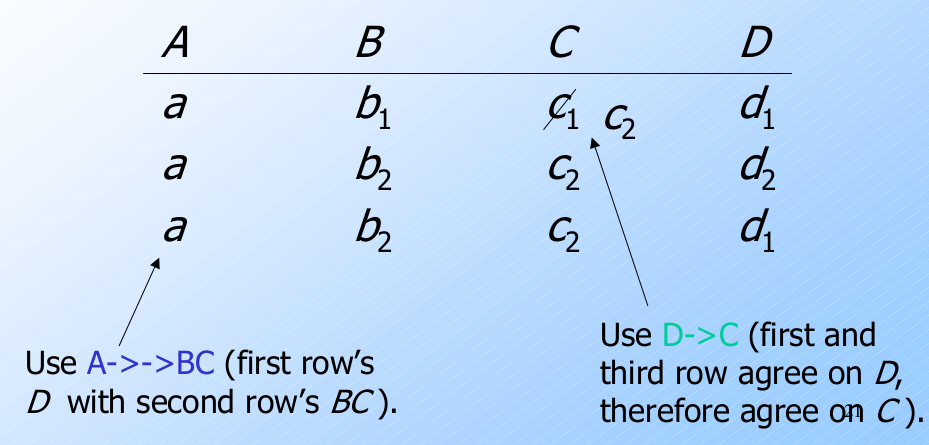
例子: MVD 的传递规则(Transitive Law for MVD's)

若 $A\rightarrow\rightarrow B$ 且 $B\rightarrow\rightarrow C$, 则 $A\rightarrow\rightarrow C$.

如果数据库模式是 $ABC$, 则根据多值依赖的互补规则, 上面的断言显然成立.
但这个断言对于其他数据模式也是成立的. 比如我们考虑关系 $R(ABCD)$.

$A\rightarrow\rightarrow C$ 的图例

目标: 推断存在元组 $(a, b_1, c_2, d_1)$.

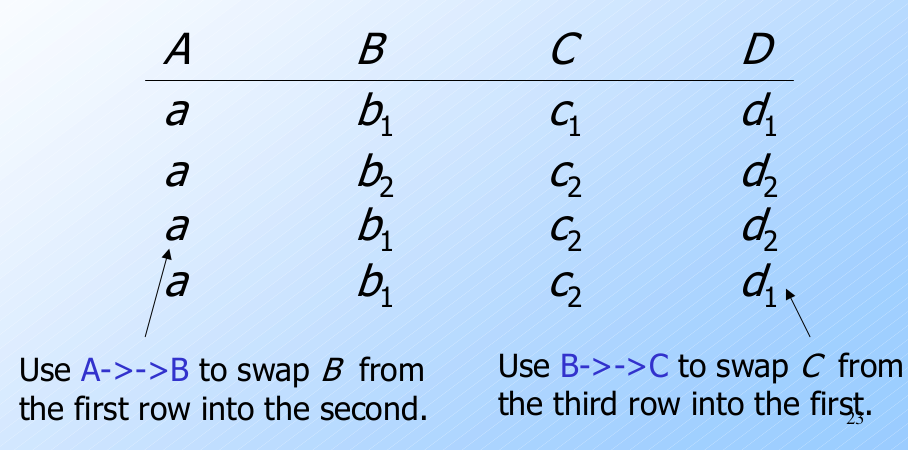
推断 MVD's+FD's 的规则

从一个具有两行的图例来说明.

这些行在要推断的依赖的左边属性集上取值是一致的.
并且它们在其他属性集上不一致.
对于取值一致的, 用没有下标的字母表示, 如果不一致则使用下标.

推断: 应用函数依赖(Inference: Applying a FD)

应用函数依赖 $X\rightarrow Y$. 找出在属性集 $X$ 上一致的行, 迫使它们在属性集 $Y$ 上取值也一致.

将一个变量用另一个替代.
若被替换的变量是目标元组的一部分, 则也替换.

推断: 应用多值依赖(Inference: Applying a MVD)

应用多值依赖 $X\rightarrow\rightarrow Y$. 对于在属性集 $X$ 上取值相同的两行,

在图例中加入那些通过交换此两行在 $Y$ 部分而得到那些行.
实际上, 就是将 $Y$ 属性组和剩余属性组 $R-X-Y$ 上的值作笛卡尔积.

Inference: Goals

为测试 $U\rightarrow V$ 是否成立, 我们接着察看 $V$ 属性组上的两个变量是否相同.

如果我们测试的是多值依赖 $U\rightarrow\rightarrow V$, 我们察看图例中的一行是否是原来的那行, 即是通过交换属性组 $V$ 上的值得到的.

Inference: Endgame

应用所有给定的 FD's 和 MVD's, 直到我们不再改变图例为止.

如果我们达到目的, 则依赖性被推出.

否则, 所得到的最后的图例是一个反例.

它满足所有给定的依赖关系.
最初的两行违反目标依赖.

End

Thanks very much!

This slide is based on Jeffrey D. Ullman's work, which can be download from his website.

感谢孙皓轩等同学指出此课件中的错误.

首页

Haifeng Xu

(hfxu@yzu.edu.cn)

目录

多值依赖(MVD)的定义

多值依赖(MVD)的定义

属性独立及随之产生的冗余

例 3.28

关系的模式和所包含的函数依赖关系

MVD 的定义

多值依赖(multivalued dependency, MVD)的定义

课本上的定义

平凡 MVD

平凡MVD(trivial MVD)

例1

例1

MVD 的传递规则

MVD 的传递规则

例子1: MVD

例 3.29: MVD

例子2: MVD

例子2: MVD

根据多值依赖$\text{name}\rightarrow\rightarrow\text{phones}$ 推出的其他元组

根据多值依赖$\text{name}\rightarrow\rightarrow\text{phones}$ 推出的其他元组

多值依赖 $X\rightarrow\rightarrow Y$ 的图解

多值依赖 $X\rightarrow\rightarrow Y$ 的图解

多值依赖的推导

多值依赖的推导

MVD 不遵循右端分解规则

MVD 的规则

MVD 的规则

分裂规则不再成立(Splitting Doesn't Hold)

分裂规则不再成立(Splitting Doesn't Hold)

例子: 右侧是多属性集(Multiattribute Right Sides)

例子: 右侧是多属性集(Multiattribute Right Sides)

例子数据

例子数据

第四范式(Fourth Normal Form)

第四范式(Fourth Normal Form)

4NF 的定义

4NF 的定义

BCNF 对比 4NF

BCNF 对比 4NF

Decomposition and 4NF

Decomposition and 4NF

例子: 4NF 分解

例子: 4NF 分解

例子: 4NF 分解 -- (2)

例子: 4NF 分解 --(2)

例子: 分解子关系 Drinkers2

例子: 分解子关系 Drinkers2

MVD's+FD's 的原因

MVD's+FD's 的原因

为什么我们要关注

为什么我们要关注

例子: 追踪含有 MVD's+FD's 的图例

例子: 追踪含有 MVD's+FD's 的图例

$A\rightarrow C$ 的图例

$A\rightarrow C$ 的图例

例子: MVD 的传递规则(Transitive Law for MVD's)

例子: MVD 的传递规则(Transitive Law for MVD's)

$A\rightarrow\rightarrow C$ 的图例

$A\rightarrow\rightarrow C$ 的图例

推断 MVD's+FD's 的规则

推断 MVD's+FD's 的规则

推断: 应用函数依赖(Inference: Applying a FD)

推断: 应用函数依赖(Inference: Applying a FD)

推断: 应用多值依赖(Inference: Applying a MVD)

推断: 应用多值依赖(Inference: Applying a MVD)

Inference: Goals

Inference: Goals

Inference: Endgame

Inference: Endgame

End