首页
函数依赖
分解
范式
Haifeng Xu
(hfxu@yzu.edu.cn)
This slide is based on Jeffrey D. Ullman's work, which can be download from his website.
如何设计关系数据库模式
如何设计关系数据库模式
人们可以采用多种方法为一个应用设计关系数据库模式.
后面会介绍描述数据结构的高层次符号, 以及将这些高层次设计转换成为关系的方法. 也可以对数据库进行需求分析进而直接定义关系, 而不必经过一些高层次的中间步骤.
无论采用哪种方式, 初始的关系模式通常都需要改进, 尤其在消除冗余方面. 一般来说, 这些问题是由于模式试图将过多的内容合并到一个关系中而造成的.
关系数据库有一个成熟的理论————依赖理论(dependency theory)
依赖理论涉及如何构建一个良好的关系数据库模式, 以及当一个模式存在缺陷时应如何改进.
- 首先从“函数依赖”(functional dependency)开始, 它是关系中“键”概念的泛化.
- 然后, 使用函数依赖这一概念来定义关系模式的规范形式. 这个称为“规范化”的理论的影响在于, 可以将关系分解为两个或多个关系以消除异常.
- 接下来介绍“多值依赖”(multivalued dependency), 它直观地表示了一个条件: 关系的一个或多个属性独立于其他若干个属性. 这些依赖也可以导致关系的规范构造和分解, 以消除冗余.
函数依赖(Functional Dependencies)
函数依赖(Functional Dependencies)
[定义]: $\mathcal{X}\rightarrow\mathcal{Y}$ 是关系 R 的一个断言(或函数依赖 FD), 指 R 中如果两个元组在属性集 $\mathcal{X}$ 上是一致的, 则必推出他们在属性集 $\mathcal{Y}$ 上也一致.
- 称 $\mathcal{X}\rightarrow\mathcal{Y}$ 在 R 上成立.
- 约定记号: ...,$\mathcal{X}$,$\mathcal{Y}$,$\mathcal{Z}$ 表示属性集; $A$,$B$,$C$,... 表示单个属性.
- 约定: 由 $A,B,C$ 三个属性构成的属性集, 一般记作 $ABC$, 而不使用通常集合的记法 {$A,B,C$}, 尽管后者比较严格.
如果确定关系 R 的每个实例都能使一个给定的 FD $f$ 为真, 那么称关系 R 满足函数依赖 $f$.
从数学上讲, 函数依赖 $f: \mathcal{X}\rightarrow\mathcal{Y}$ 实际上就是指 $f: \mathcal{X}\rightarrow\mathcal{Y}$ 是一个映射.
对函数依赖的右边属性集进行分解
对函数依赖的右边属性集进行分解
$\mathcal{X}\rightarrow A_1A_2\ldots A_n$ 对于关系 R 成立当且仅当 $\mathcal{X}\rightarrow A_1$, $\mathcal{X}\rightarrow A_2$, ..., $\mathcal{X}\rightarrow A_n$ 对于关系 R 都成立.
或者写为: 一个函数依赖 $A_1 A_2\ldots A_n\rightarrow B_1 B_2\ldots B_m$ 等价于一组 FD:
\[
\begin{aligned}
A_1 A_2\ldots A_n&\rightarrow B_1,\\
A_1 A_2\ldots A_n&\rightarrow B_2,\\
&\cdots\\
A_1 A_2\ldots A_n&\rightarrow B_m,\\
\end{aligned}
\]
例子: $A\rightarrow BC$ 等价于 $A\rightarrow B$ 且 $A\rightarrow C$.
但对于函数依赖(FD) 左边的属性集, 则没有这样的分解规则.
我们一般将函数依赖(FD) 表示成右侧是单属性集的函数依赖.
例子: FD's
例子: FD's
Drinkers(name,addr,beersLiked,manf,favBeer)
合理的函数依赖是这样声明的:
- $\text{name}\rightarrow \text{addr favBeer}$
- 注意到这个函数依赖与 $\text{name}\rightarrow \text{addr}$ 且 $\text{name}\rightarrow \text{favBeer}$ 是一致的.
- $\text{beersLiked}\rightarrow\text{manf}$
例子: Possible Data
例子: 可以出现的数据
| name |
addr |
beersLiked |
manf |
favBeer |
| Janeway |
Voyager |
Bud |
A.B. |
WickedAle |
| Janeway |
Voyager |
WickedAle |
Pete's |
WickedAle |
| Spock |
Enterprise |
Bud |
A.B. |
Bud |
- $\text{name}\rightarrow\text{addr}$
- $\text{name}\rightarrow\text{favBeer}$
- $\text{beersLiked}\rightarrow\text{manf}$
关系的键
关系的键
设 $\mathcal{A}=\{A_1,A_2,\ldots,A_n\}$ 是关系 R 的所有属性构成的属性集, $\mathcal{K}\subset\mathcal{A}$.
- $\mathcal{K}$ 是关系 R 的一个超键(superkey), 如果 $\mathcal{K}$ 可以函数决定关系 $\mathcal{A}$, 即 R 的所有属性.
- $\mathcal{K}$ 是关系 R 的一个键(key), 如果 $\mathcal{K}$ 的任何真子集都不是 R 的一个超键. 也就是说, 键必须是最小的. 键是最小的超键.
或者先定义键. 考虑关系 $R(\mathcal{A})$, $\mathcal{A}=\{A_1,A_2\ldots,A_n\}$ 是属性集.
- 若存在 $\mathcal{K}\subset\mathcal{A}$, 使得 $\mathcal{K}\rightarrow\mathcal{A}$ 且 $\mathcal{K}\setminus\{A_j\}\not\rightarrow\mathcal{A}$ 对任意 $j=1,2,\ldots,n$, 则称 $\mathcal{K}$ 是关系 $R(\mathcal{A})$ 的一个键(key). 注意键不一定唯一.
- 若 $\mathcal{K}$ 是键, 则以 $\mathcal{K}$ 为子集的任何属性集都称为关系 $R(\mathcal{A})$ 的超键(superkey)
当键 $\mathcal{K}$ 只包含一个属性 $A$时, 我们通常称 $A$ (而不是 $\{A\}$) 是键.
例子: 超键(superkey)
例子: 超键(superkey)
Drinkers(name,addr,beersLiked,manf,favBeer)
{name,beersLiked} 是一个超键, 因为这两个属性可以函数决定其他三个属性.
- $\text{name}\rightarrow\text{addr favBeer}$
- $\text{beersLiked}\rightarrow\text{manf}$
例子: 键(key)
例子: 键(key)
{name,beersLiked} 是一个键, 因为不论 {name} 还是 {beersLiked} 都不是超键.
- $\text{name}\not\rightarrow\text{manf}$
- $\text{beersLiked}\not\rightarrow\text{addr}$
没有其他的键了, 但有很多超键.
- 任何包含 {name,beersLiked} 的集合都是超键.
Where Do Keys Come From
键从哪里来
- 键 $K$.
- 键 $K$ 必须满足函数依赖 $K\rightarrow A$, $A$ 是关系中的所有属性.
- 根据具体关系, 从语义上判断探索其中的函数依赖, 并导出所有可能的键.
More FD's From "Physics"
More FD's From "Physics"
更多来源于现实世界的函数依赖例子.
例子: 没有哪个课是可以在同一时间同一教室上的. 因此这告诉我们
$\text{DataTime room}\rightarrow\text{course}$
函数依赖的规则
函数依赖的推导(Inferring FD's)
假设已经知道某个关系满足一些FD集合,从这些已知的FD中还能推出在这个关系上存在的其他FD。
假设在某个关系上存在 FD 集合: $X_1\rightarrow A_1$, $X_2\rightarrow A_2$, ... , $X_n\rightarrow A_n$. 我们想知道此关系是否也成立 $Y\rightarrow B$.
这对于设计好的关系模式非常重要.
例如: 若 $A\rightarrow B$ 且 $B\rightarrow C$, 则一定推出 $A\rightarrow C$.
在不改变关系合法实例集合的前提下,FD可以有多种不同的描述方法:
- 对于FD集合S和T, 若关系实例集合满足S与满足T的情况完全一样,就认为S和T是等价的(equivalent),记为 $S\cong T$
- 若满足T中所有FD的每个关系实例也满足S中的所有FD,则认为S是从T中推断(follow)而来,记为 $T\Rightarrow S$
- $T\Rightarrow S$ and $S\Rightarrow T\ \Leftrightarrow T\cong S$.
设 $T=\{FD_i\mid FD_i: A_1A_2\ldots A_n\rightarrow B_i, i=1,2,\ldots,m\}$, $S=\{FD: A_1A_2\ldots A_n\rightarrow B_1B_2\ldots B_m\}$
显然 $T\cong S$.
如果用T代替S,则称为分解规则(splitting rule).
如果用S代替T,则称为结合规则(combining rule).
例子:
\[
\begin{aligned}
&\text{title year} \rightarrow \text{length}\\
&\text{title year} \rightarrow \text{genre}\\
&\text{title year} \rightarrow \text{studioName}\\
\end{aligned}
\]
与单个FD
\[
\text{title year} \rightarrow \text{length genre studioName}
\]
等价
推理测试(Inference Test)
推理测试(Inference Test)
为测试 $Y\rightarrow B$, 假设有两个元组关于 $Y$ 的所有属性都一致.

推理测试 (2)
推理测试 (2)
利用给定的函数依赖(FD's), 推出这些元组在某些其他属性上也一致.
- 若 $B$ 是这些属性中的一个, 则 $Y\rightarrow B$ 成立.
- 若 $B$ 不是这些属性中的一个, 则这两个元组(可能带有任意其他的强制相等)组成的一个关系满足 $Y\rightarrow B$ 但这并不是由这些 FD's 导出的.
平凡函数依赖
平凡函数依赖
如果 $\{B_1,B_2,\ldots,B_m\}\subset\{A_1,A_2,\ldots,A_n\}$, 则称函数依赖
\[
FD:\ A_1 A_2 \ldots A_n\rightarrow B_1 B_2 \ldots B_m
\]
是一个平凡依赖.
也就是说平凡FD是说“两个元组在属性 $A_1,A_2,\ldots,A_n$ 上取值相同,则它们在这 $n$ 个属性的任一子集上取值都相同”.
闭包测试(Closure Test)
闭包测试(Closure Test)
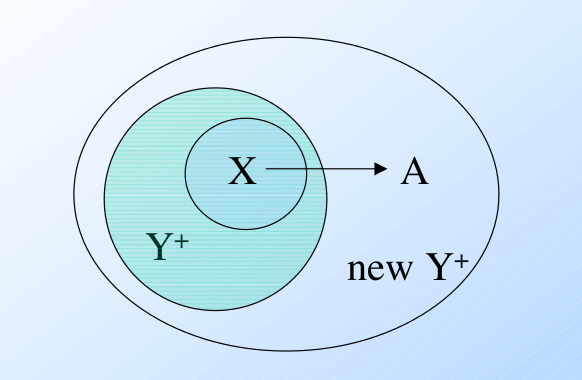
一个容易的测试方式是计算 $Y$ 的闭包(closure), 记作 $Y^+$.
首先基于原来的属性集, 即令 $Y^+=Y$.
然后是归纳: 检查函数依赖(FD)的左边的属性集 $X$, 它是 $Y^+$ 的子集. 如果 FD 是 $X\rightarrow A$, 则将 $A$ 加入到 $Y^+$ 中.
Finding All Implied FD's
Finding All Implied FD's
动机: "normalization", 我们将一个关系模式分解为两个或更多的模式的过程.
例子: $ABCD$, 函数依赖集合为 $AB\rightarrow C$, $C\rightarrow D$, $D\rightarrow A$.
- 分解为 $ABC$, $AD$. 在 $ABC$ 中哪些函数依赖还成立?
- 不仅 $AB\rightarrow C$, 而且 $C\rightarrow A$ 也成立.
Why?
Why?
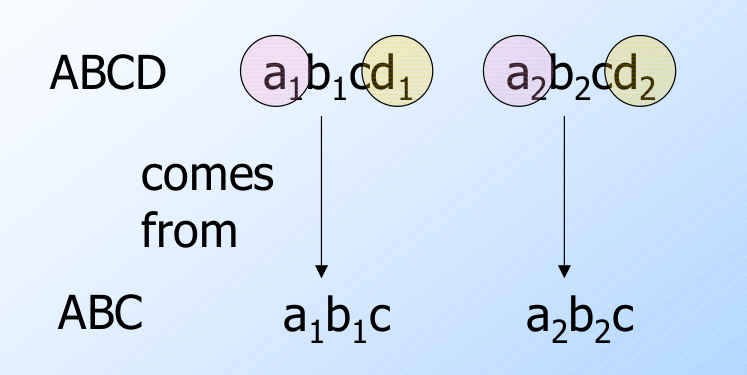
- $d_1=d_2$ 是因为 $C\rightarrow D$.
- $a_1=a_2$ 是因为 $D\rightarrow A$.
- 于是, 投影中的 $C$ 属性相等的两个元组在 $A$ 上也是相等的. 因为 $C\rightarrow A$.
基本思想
基本思想
从给定的函数依赖出发, 找出所有可以从给定函数依赖(FD's)导出的非平凡的(nontrivial)的函数依赖.
- 非平凡的(nontrivial): 指右边不包含在左边.
当限制在这些函数依赖时, 它们仅涉及投影模式中的属性.
Simple, Exponential Algorithm
Simple, Exponential Algorithm
- 对每个属性集 $X$, 计算它的闭包 $X^+$.
- 对所有 $X^+-X$ 中的 $A$, 添加 $X\rightarrow A$.
- 每当发现有 $X\rightarrow A$ 成立时, 就舍去 $XY\rightarrow A$.
- 因为 $XY\rightarrow A$ 可以从 $X\rightarrow A$ 导出.
- 最后, 利用函数依赖包含投影属性的规则.
一些小技巧
一些小技巧
没有必要去计算空集或是所有属性组成集合的闭包.
如果我们发现 $X^+$ 等于所有属性, 则它是包含 $X$ 的任何集合的闭包.
例子: 函数依赖的投影
例子: 函数依赖的投影
考虑属性集 $ABC$, 函数依赖是: $A\rightarrow B$, $B\rightarrow C$. 将它们投影到 $AC$ 上.
- $A^+=ABC$; 推出 $A\rightarrow B$, $B\rightarrow C$.
- 我们没有必要再去计算 $\{AB\}^+$ 或 $\{AC\}^+$.
- $B^+=BC$; 推出 $B\rightarrow C$.
- $C^+=C$; yields nothing.
- $\{BC\}^+=BC$; yields nothing.
- 最终所得到的函数依赖集为: $A\rightarrow B$, $A\rightarrow C$ 及 $B\rightarrow C$.
- 投影到 $AC$ 上, 则函数依赖集为: $A\rightarrow C$.
函数依赖的几何观点
函数依赖的几何观点
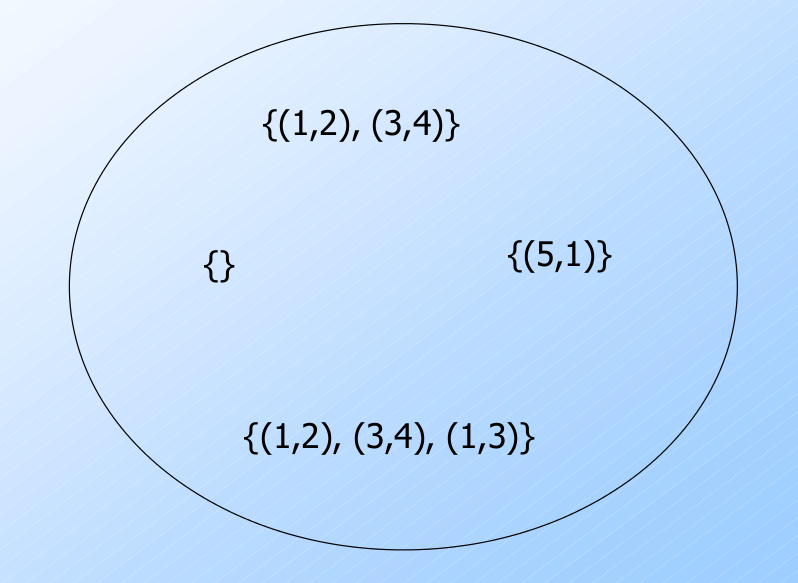
将一个特定关系的所有实例(instances)组成一个集合.
也就是说, 具有相同组成部分的有限元组构成一个实例, 考虑所有这样的实例集合.
将每个实例认为是该空间中的一个点.
例子: R(A,B)
函数依赖是实例构成的子集
函数依赖是实例构成的子集
对每个函数依赖(FD) $X\rightarrow A$, 存在某个子集满足此 FD.
我们可以用这个空间中的某个区域来表示这个函数依赖.
平凡的函数依赖=由整个空集所代表的函数依赖.
例子: $A\rightarrow B$ for R(A,B)
例子: $A\rightarrow B$ for R(A,B)

FD 的表示集(Representing Sets of FD's)
FD 的表示集(Representing Sets of FD's)
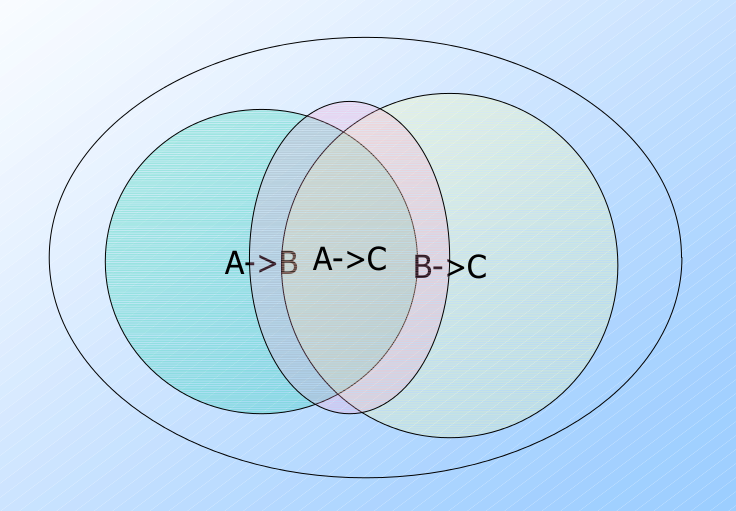
如果每个函数依赖(FD)是一些关系实例的集合, 则函数依赖集合对应到这些关系实例子集的交集.
- 之所以是交集是因为所有这些实例必须满足所有的函数依赖.
例子
例子

函数依赖的推断(Implication of FD's)
函数依赖的推断(Implication of FD's)
如果一个 FD $Y\rightarrow B$ 可从函数依赖集合 $X_1\rightarrow A_1$, ..., $X_n\rightarrow A_n$ 推出, 则关于 $Y\rightarrow B$ 的关系实例空间必包含这些函数依赖 $X_j\rightarrow A_j$ 所对应的区域的交集.
- 也就是说, 任何满足函数依赖集合 $\{X_j\rightarrow A_j\}_{i=1}^n$ 的关系实例必定满足 $Y\rightarrow B$.
- 但可能存在满足 $Y\rightarrow B$ 的实例, 却不在那个交集中.
函数依赖的完备化
例子
例子
关系模式设计(Relational Schema Design)
关系模式设计(Relational Schema Design)
关系模式设计的目标是避免异常(anomalies)和冗余(redundancy).
- 更新异常(update anomaly): one occurrence of a fact is changed, but not all occurrences.
- 删除异常(delete anomaly): valid fact is lost when a tuple is deleted.
例子: 糟糕的设计
例子: 糟糕的设计
Drinkers(name,addr,beersLiked,manf,favBeer)
| name |
addr |
beersLiked |
manf |
favBeer |
| Janeway |
Voyager |
Bud |
A.B. |
WickedAle |
| Janeway |
??? |
WickedAle |
Pete's |
??? |
| Spock |
Enterprise |
Bud |
??? |
Bud |
- 数据冗余, 因为每个 ??? 可以由函数依赖集 $\text{name}\rightarrow\text{addr favBeer}$ 和 $\text{beersLiked}\rightarrow\text{manf}$ 推出.
这个糟糕的设计也给我们展示了异常
这个糟糕的设计也给我们展示了异常
| name |
addr |
beersLiked |
manf |
favBeer |
| Janeway |
Voyager |
Bud |
A.B. |
WickedAle |
| Janeway |
Voyager |
WickedAle |
Pete's |
WickedAle |
| Spock |
Enterprise |
Bud |
A.B. |
Bud |
- 更新异常(update anomaly): 如果 Janeway 搬迁到另一个地方, 我们还记得要更新她的其他元组?
- 删除异常(delete anomaly): 如果没有人喜欢 Bud 啤酒, 那我们就丢失了 Anheuser-Busch 生产 Bud 啤酒的记录.
Boyce-Codd 范式(Boyce-Codd Normal Form)
Boyce-Codd 范式(Boyce-Codd Normal Form)
我们称一个关系 R 是 BCNF 的, 如果对于关系 R 的每个非平凡函数依赖 $\mathcal{X}\rightarrow\mathcal{Y}$, $\mathcal{X}$ 是一个超键.
- 回忆: 非平凡(nontrivial)意指 $\mathcal{Y}$ 不包含在 $\mathcal{X}$ 中.
- 回忆: 超键(superkey) 是指键的任意一个超集(superset). 不要求真包含键(not necessarily a proper superset).
例子
例子
Drinkers(name,addr,beersLiked,manf,favBeer)
函数依赖集是: $\text{name}\rightarrow\text{addr favBeer}$, $\text{beersLiked}\rightarrow\text{manf}$
- 仅可以成为键的是 {name,beersLiked}
- 在每个函数依赖表达式中, 左边都不能构成一个超键.
- 这里的任何一个函数依赖表明 Drinkers 关系不是 BCNF 的.
另一个例子
另一个例子
Beers(name,manf,manfAddr)
函数依赖集是: $\text{name}\rightarrow\text{manf}$, $\text{manf}\rightarrow\text{manfAddr}$.
- 仅可以成为键的是 {name} .
- $\text{name}\rightarrow\text{manf}$ 并没有违反 BCNF, 但是 $\text{manf}\rightarrow\text{manfAddr}$ 却违反了 BCNF.
分解为 BCNF
分解为 BCNF
给定关系 R 和函数依赖集 $\mathcal{F}$.
从给定的函数依赖集中寻找违反 BCNF 的 FD $\mathcal{X}\rightarrow\mathcal{Y}$.
- Prop. 如果从函数依赖集 $\mathcal{F}$ 推出的某个 FD 违反了 BCNF, 则 $\mathcal{F}$ 自身必包含一个违反 BCNF 的 FD.
写成数学的语言: 记函数依赖集为 $\mathcal{F}:=\mathrm{FDs}$. $\overline{\mathcal{F}}$ 是 $\mathcal{F}$ 的完备化, 即 $\mathcal{F}$ 的所有导出的函数依赖的集合.
- Prop. 若存在 $f\in\overline{\mathcal{F}}$, $f\not\in\mathrm{BCNF}$, 则必存在 $g\in\mathcal{F}$, $g\not\in\mathrm{BCNF}$.
计算 $\mathcal{X}^+$.
- 注意 $\mathcal{X}^+\not\subset\mathcal{A}$, $\mathcal{A}$ 指所有属性构成的集合. 否则 $\mathcal{X}$是一个超键. (与假设 $\mathcal{X}\rightarrow\mathcal{Y}$ 违反 BCNF 矛盾.)
利用 $\mathcal{X}\rightarrow\mathcal{Y}$ 分解关系 R
利用 $\mathcal{X}\rightarrow\mathcal{Y}$ 分解关系 R
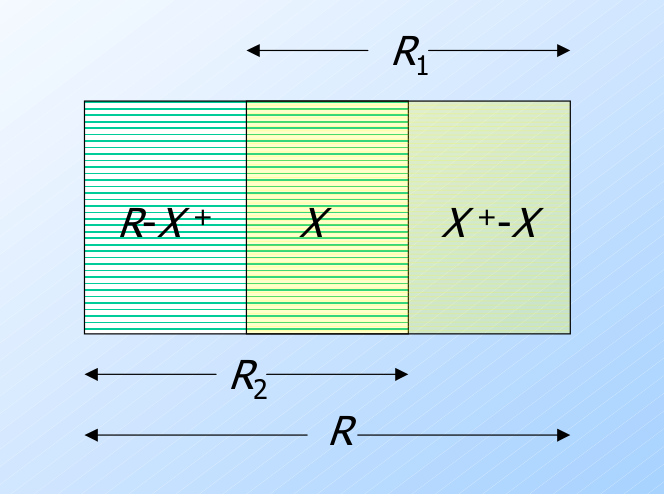
将关系 $R$ 替换为下面模式的两个关系 $R_1(\mathcal{R}_1)$ 和 $R_2(\mathcal{R}_2)$:
- $\mathcal{R}_1=\mathcal{X}^+$ .
- $\mathcal{R}_2=\mathcal{R}-(\mathcal{X}^{+}-\mathcal{X})$ .
这里 $\mathcal{R}$ 是指关系 $R$ 中所有属性构成的集合.
将给定的函数依赖集 $\mathcal{F}$ 投影(Project) 到这两个新的关系上.
分解示意图
分解示意图
例子: BCNF 分解
例子: BCNF 分解
Drinkers(name,addr,beersLiked,manf,favBeer)
函数依赖集
\[
\begin{split}
\mathcal{F}=\{&\text{name}\rightarrow\text{addr},\\
&\text{name}\rightarrow\text{favBeer},\\
&\text{beersLiked}\rightarrow\text{manf}\}
\end{split}
\]
- 找出一个违反 BCNF 的函数依赖 $\text{name}\rightarrow\text{addr}$.
- 计算左边 {name} 的闭包:
$\{\text{name}\}^+=\{\text{name,addr,favBeer}\}$.
- 按照 $\mathcal{X}^+$ 和 $\mathcal{R}-(\mathcal{X}^{+}-\mathcal{X})$ 分解关系 Drinkers:
- Drinkers1(name,addr,favBeer)
- Drinkers2(name,beersLiked,manf)
Example -- Continued
Example -- Continued
我们还没有完成; 我们必须检验 Drinkers1 和 Drinkers2 是否是 BCNF 的.
此时函数依赖集的投影比较简单.
对应 Drinkers1(name,addr,favBeer), 相关的函数依赖是 $\text{name}\rightarrow\text{addr}$ 和 $\text{name}\rightarrow\text{favBeer}$.
- 于是, {name} 是仅可以成为键的属性集, 因此 Drinkers1 是 BCNF 的.
Example -- Continued
Example -- Continued
对应 Drinkers2(name,beersLiked,manf), 仅有的函数依赖是: $\text{beersLiked}\rightarrow\text{manf}$, 且仅可能成为键的属性集是 {name,beersLiked}.
我们按照上面的规则继续分解关系 Drinkers2.
$\text{beersLiked}^+=\{\text{beersLiked,manf}\}$, 因此我们可以将关系 Drinkers2 分解为
- Drinkers3(beersLiked,manf)
- Drinkers4(name,beersLiked)
Example -- Concluded
Example -- Concluded
关系 Drinkers 最终的分解是:
- Drinkers1(name,addr,favBeer)
- Drinkers3(beersLiked,manf)
- Drinkers4(name,beersLiked)
这里我们所有的表都满足 BCNF.
注意:
- Drinkers1 告诉我们关于酒客的信息.
- Drinkers3 告诉我们关于啤酒的信息.
- Drinkers1 告诉我们关于酒客和他喜欢的啤酒的信息.
我们看到, 如果遵循 BCNF 范式, 那么所分解后的数据库模式与我们从直觉上设计的模式(实体作为单独对象, 实体与实体之间的联系也设计为一张表)是相符的.
第三范式(Third Normal Form) -- 动机
第三范式(Third Normal Form) -- 动机
存在一种函数依赖结构, 它将会在我们分解关系时导致困难.
例子
假设关系 $R(A,B,C)$ 具有函数依赖集合: $AB\rightarrow C$ 和 $C\rightarrow B$.
- 实际的例子: $A$=streetAddress, $B$=city, $C$=zipcode.
注意
- 同一个城市不允许有重名的街道地址;
- 相同邮政编码的区域一般包含很多街道;
- 同一个城市的不同区有不同的邮政编码, 并且邮政编码在全国范围是唯一的, 可以从邮政编码推出所在地区是属于哪个城市.
- 城市可能有重名(比如美国有许多重名的城市: Burlington, Milford, Newport, Chester, Riverside, Oxford, Ashland, Milton, Springfield, Manchester,Clayton, Georgetown, Arlington, Marion, Madison, Greenville, Clinton, Fairview, Franklin).
Ref. http://vhouse.163.com/17/0719/11/CPN10V2V002988JQ.html
这里可以有两个键: $\{A,B\}$ 和 $\{A,C\}$. (可见键不一定是唯一的.)
所给的函数依赖 $C\rightarrow B$ 违反了 BCNF, 因此如果要满足 BCNF, 我们必须把关系 $R(ABC)$ 分解为 $R(AC)$ 和 $R(BC)$.
- 事实上: $\{C\}^+=\{B,C\}$, 因此 $\{A,B,C\}-\{\{C\}^{+}-\{C\}\}=\{A,C\}$.
We cannot enforce FD's
We cannot enforce FD's
问题在于如果我们使用 $AC$, $BC$ 作为数据库模式, 则我们不能在分解后的关系中通过检验函数依赖来执行函数依赖 $AB\rightarrow C$.
下面的例子解释了这一点, 其中设 $A$=streetAddress, $B$=city, $C$=zipcode.
例子: 一个不能执行的函数依赖
例子: 一个不能执行的函数依赖
| streetAddress |
zipcode |
| 545 Tech Sq. |
02138 |
| 545 Tech Sq. |
02139 |
| city |
zipcode |
| Cambridge |
02138 |
| Cambridge |
02139 |
将这两个表按照 zipcode 作自然连接.
| streetAddress |
city |
zipcode |
| 545 Tech Sq. |
Cambridge |
02138 |
| 545 Tech Sq. |
Cambridge |
02139 |
- 尽管在分解后的关系中, 不存在违反 BCNF, 但是函数依赖 $\text{streetAddress city}\rightarrow\text{zipcode}$ 在整个数据库中失效了.
3NF 可以使我们避免这个问题
3NF 可以使我们避免这个问题
第三范式(Third Normal Form)将 BCNF 的条件稍微放松了一下, 以允许那些在分解为 BCNF 关系时不能保持函数依赖的特殊关系模式.
称某个属性是主属性(prime attribute), 如果它是任何一个键的成员.
$\mathcal{X}\rightarrow A$ 违反 3NF 当且仅当 $\mathcal{X}$ 不是一个超键, 并且 $A$ 也不是一个主属性.
- 换句话说, 3NF 的条件可以表述为: 对于每个非平凡的 FD, 或者其左边是超键, 或者其右边仅由主属性构成.
- 3NF 的条件要比 BCNF 的条件要弱. 属于 BCNF 的一定是 3NF 的.
例子: 3NF
例子: 3NF
在我们的问题中, 函数依赖集是: $AB\rightarrow C$ 和 $C\rightarrow B$. 我们可以有键 $AB$ 和 $AC$.
于是 $A$, $B$, $C$ 都是主属性.
尽管 $C\rightarrow B$ 违反了 BCNF, 但它不违反 3NF.
What 3NF and BCNF Give You
What 3NF and BCNF Give You
分解有两个重要的性质:
- 无损连接(Lossless Join): 应当可以将原始关系投影到分解后的关系模式上, 并且可以通过分解后的关系重构原始关系.
- 依赖保持(Dependency Preservation): 在投影后的关系中应当可以检验是否所有给定的函数依赖都被保持.
- BCNF 分解可以保证 (1).
- 但是 BCNF 分解不能总是可以保证 (2).
- 3NF 分解可以保证 (1) 和 (2).
无损连接的测试
无损连接的测试
如果我们将关系 $R$ 分解为 $R_1,R_2,\ldots,R_k$, 我们还能通过连接来恢复关系 $R$ 吗?
$R$ 中的任意一个元组都能够从投影后的片段中恢复.
因此仅有的问题是:
- 当我们重新连接时, 我们是否得到了不属于最初的东西?
追踪检测(The chase test)
追踪检测(The chase test)
假设元组 t 来自于重新连接后的关系.
则 t 是关系 $R$ 中某些元组投影后的重新连接元组. 每个投影部分是属于分解后的关系 $R_i$.
我们是否可以使用给定的函数依赖集合去证明这些(连接后的)元组之一必是 t?
追踪检测(The chase test) -- (2)
追踪检测(The chase test) -- (2)
假设 t=abc...
对每个 $i$, 存在 $R$ 中的一个元组 $s_i$ 使得 $a,b,c,\ldots$ 出现在 $R_i$ 的属性集合中.
$s_i$ 在其他属性上可能有其他值.
我们将使用在 t 中一样的字母, 但对于组成部分会有一个下标.
例子: 追踪(The Chase)
例子: 追踪(The Chase)
设 $R=ABCD$,
设给定的函数依赖是 $C\rightarrow D$ 和 $B\rightarrow A$.
容易验证, 按照给定的函数依赖, 如果按照 BCNF 的分解规则, 则分解为 $AB$, $BC$, $CD$.
假设元组 $t=abcd$ 是由投影到 $AB$, $BC$, $CD$ 上的元组连接后得到的.
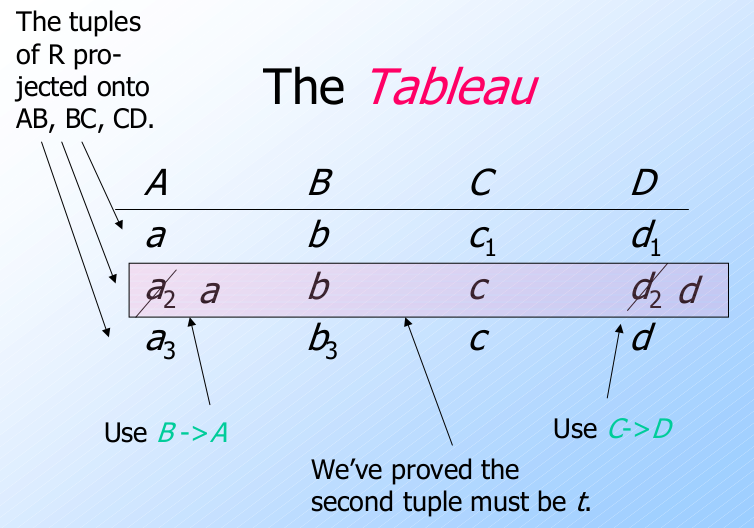
图例(The Tableau)
图例(The Tableau)
Summary of the Chase
Summary of the Chase
- 如果两个元组对于某个函数依赖FD的左边是一致的, 则将他们在右边的值也使得一致.
- 如果可能, 总是将标有下标的符号用没有下标的符号来代替.
- 如果我们得到一行都是没有下标的, 则我们知道在投影-连接(project-join)中的任一元组都是原始关系中的.(即连接是无损连接.)
- 否则, 最后的图例是一个反例.
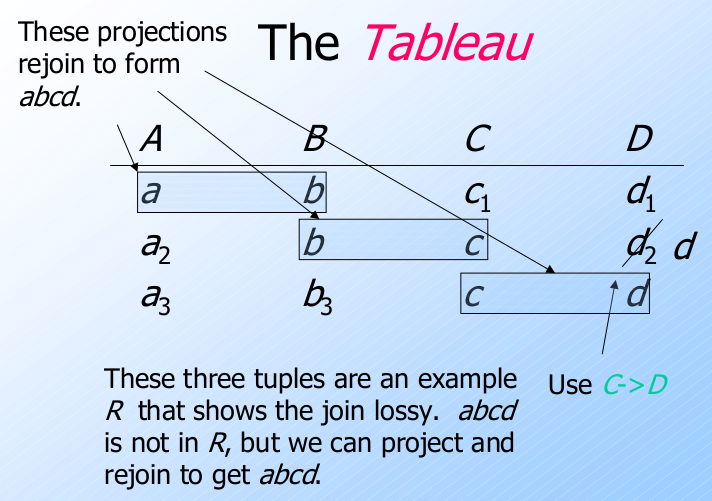
例子: 有损连接(Lossy Join)
例子: 有损连接(Lossy Join)
考虑与刚才同样的关系 $R=ABCD$, 及相同的分解(分解为 $AB$, $BC$, $CD$).
但只有一个函数依赖: $C\rightarrow D$.
图例(The Tableau)--2
图例(The Tableau)--2
3NF 合成算法(3NF Synthesis Algorithm)
3NF 合成算法(3NF Synthesis Algorithm)
我们总是能够将关系分解为符合 3NF 的子关系, 并且是无损连接的和保持函数依赖的.
FD 的最小化基本集(minimal basis)是指
- 函数依赖的右边是单属性.
- 不可以去除任何一个 FD, 否则与所给函数依赖集不等价.
- 任一函数依赖的左边属性集是最小化的, 也就是说无法再去除某个属性.
构造一个最小化基本集(Constructing a Minimal Basis)
构造一个最小化基本集(Constructing a Minimal Basis)
首先将函数依赖集中的每个 FD 分解成右侧都是单属性的 FD.
试着去除某个 FD, 看余下的函数依赖集是否与原来的等价, 如果等价, 就删除此 FD. 重复这个过程.
对于某个 FD, 试着去除其左侧属性集中的某个属性, 看得到的函数依赖集与原先的是否等价. 如果等价, 就去除此属性. 不断重复这个过程, 直到不能再去除为止.
3NF Synthesis – (2)
3NF Synthesis – (2)
对于最小化基本集中的每个函数依赖 FD, 建立与之对应的关系.
如果某个 FD 不包含键, 则增加一个关系, 其模式是某个键.
例子: 3NF Synthesis
例子: 3NF Synthesis
考虑关系 $R=ABCD$.
函数依赖集合是: $A\rightarrow B$, $A\rightarrow C$.
分解:
- 所给函数依赖集合即最小化基本集. 因此建立两个关系 $AB$ 和 $AC$.
- 由于分解出的关系模式中均不包含原关系的 $R$ 的超键, 因此添加一个关系 $AD$, 它是一个键.
为什么 3NF 综合算法有效
为什么 3NF 综合算法有效
依赖保持性(Preserves dependencies): 每个来自于最小化基本集中的函数依赖都为之建立了对应的关系, 因此函数依赖是保持的.
无损连接(Lossless Join): 利用追踪检验可以证明.
3NF: 这是最小化基本集的一个性质. (难点)
End
Thanks very much!
This slide is based on Jeffrey D. Ullman's work, which can be download from his website.










